Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Elípticas

Ver Teoria
Exercício 123456789101112131415

Enunciado

Sabendo que D é a região em que   | y | ≤ x e que 1 ≤ x ≤ 2 , calcule a seguinte integral dupla

I = ∬ D   d x d y x 2 + 9 y 2 3 2  

Passo 1

Os termos quadráticos no denominador da integral são um indicativo de que devemos usar coordenadas elípticas (os coeficientes são diferentes). Mas que substituição faremos, se não temos uma elipse? Vamos buscar uma mudança que simplifique o denominador, transformando-o em r 2 . Seguindo o mesmo raciocínio que fizemos com as elipses, se chamarmos a = 1 e b = 1 / 3 , teremos:

x = a r cos ⁡ θ = r cos ⁡ θ

y = b r   s e n θ = r 3 s e n θ

J = a b   r = r 3

Passo 2

Agora vamos calcular os limites de integração, substituindo os valores que definimos para x e y nas expressões do domínio:

y ≤ x → - x ≤ y ≤ x

- r cos ⁡ θ ≤ r 3 s e n θ ≤ r cos ⁡ θ

Dividindo tudo por r e por cos ⁡ θ

- r cos ⁡ θ r cos ⁡ θ ≤ 1 3 r sen ⁡ θ r cos ⁡ θ ≤ r cos ⁡ θ r cos ⁡ θ

- 3 ≤ t g   θ ≤ 3

Os ângulos que possuem essas tangentes são   θ = arctg ⁡ 3 e θ = arctg ⁡ - 3 , portanto

arctg ⁡ ( - 3 ) ≤ θ ≤ arctg ⁡ 3

1 ≤ x ≤ 2   → 1 ≤ r cos ⁡ θ ≤ 2  

sec ⁡ θ ≤ r ≤ 2 sec ⁡ θ

Podemos escrever, então:

D * = { ( r , θ ) | arctg ⁡ - 3 ≤ θ ≤ arctg ⁡ 3 ;   sec ⁡ θ ≤ r ≤ 2 sec ⁡ θ }

Passo 3

Substituindo tudo na integral e não esquecendo do jacobiano, ficamos com,

I = 1 3 ∬ D *   r   d r d θ r cos ⁡ θ 2 + 9 r 3 s e n θ 2 3 / 2 =

= 1 3 ∬ D *   r   d r d θ r 2 3 / 2 =

= 1 3 ∬ D *     d r d θ r 2

Passo 4

Agora vamos montar a integral em termos de r e θ :

1 3 ∫ arctg ⁡ - 3 arctg ⁡ 3   ∫ sec ⁡ θ 2 sec ⁡ θ d r d θ r 2 =

Passo 5

Integrando em relação a r , temos:

= - 1 3 ∫ arctg ⁡ - 3 arctg ⁡ 3   1 r sec ⁡ θ 2 sec ⁡ θ d θ =

= - 1 3 ∫ arctg ⁡ - 3 arctg ⁡ 3 cos ⁡ θ 2 - cos ⁡ θ   d θ =

Passando o sinal de menos, fora da integral, para dentro, fica assim

= 1 3 ∫ arctg ⁡ - 3 arctg ⁡ 3 cos ⁡ θ 2   d θ =

= 1 6 ∫ arctg ⁡ - 3 arctg ⁡ 3 cos ⁡ θ   d θ =

Passo 6

Integrando, agora, em relação a θ , temos:

= 1 6 s e n   θ arctg ⁡ - 3 arctg ⁡ 3 d θ =

= 1 6 sen ⁡ arctg ⁡ 3 - sen ⁡ arctg ⁡ - 3

Mas sabemos que arctg ⁡ - 3 = - arctg ⁡ 3 :

= 1 6 sen ⁡ arctg ⁡ 3 - sen ⁡ - arctg ⁡ 3

E sabemos que sen ⁡ - arctg ⁡ 3 = - sen ⁡ arctg ⁡ 3 :

= 1 6 sen ⁡ arctg ⁡ 3 + sen ⁡ arctg ⁡ 3

= 1 3 sen ⁡ arctg ⁡ 3

Mas qual o seno do arco que tem tangente igual a 3 ? Você pode usar as equações trigonométricas para calcular, mas isso pode ser um pouco trabalhoso. Aqui vai uma dica que é bem mais prática:

  1. Desenhe um triângulo retângulo e chame um dos seus ângulos agudos de θ ;
  2. Escreva nele a informação que você tem, no caso, t g   θ = 3 . Mas como? A forma mais simples é colocar 3 no cateto oposto a θ e 1 no cateto adjacente;
  3. Falta um lado, certo? Calcule o valor dele usando Pitágoras ( a 2 = b 2 + c 2 );
  4. Pronto, agora você consegue calcular o que quiser fazendo a razão entre os lados do triângulo. Nesse caso, sen ⁡ θ = cateto oposto hipotenusa

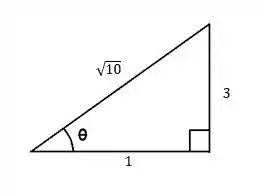
Pra recapitular melhor, sabemos que o “arco com tangente igual a 3 ” é θ , portanto

θ = arctg ⁡ 3

Portanto, quando queremos saber sen ⁡ arctg ⁡ 3 queremos na verdade sen ⁡ θ

Então, temos que s e n   θ = 3 10 . Substituindo:

= 1 3 sen ⁡ arctg ⁡ 3 = 1 3 . 3 10 = 1 10 = 10 10  

Resposta

10 10

Exercícios de Livros Relacionados

Seja σ θ ,ρ = 2 ρ cos ⁡ θ ,ρ s e nθ . Mostre que σ transforma a reta ρ = 1 numa elipse. Desenhe tal elipse.
Calcule a área da região delimitada pela elipse
Seja σ a transformação do Exercício 10. Desenhe σ ( B ) onde B é o retângulo 0 ≤ ρ ≤ 1 , 0 ≤ θ ≤ 2 π .