Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Elípticas

Ver Teoria
Exercício 121234567891011131415

Enunciado

Questão 1: Calcule a área da região plana R = x ,   y   |   2 x 2 + y 2 ≤ 6 ,   2 x 2 + y 2 ≤ 4 x .

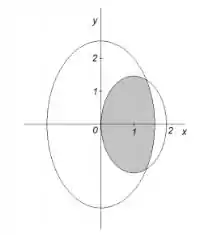
(Dica: Fazer uma mudança de variáveis compatível com a equação da maior elipse).

Passo 1

Vamos começar o nosso problema entendendo um pouquinho como podemos chegar ao resultado. Sabemos que toda área pode ser calculada utilizando uma integral dupla:

A = ∬ R   1 d A

Onde R é a região a qual buscamos a sua área:

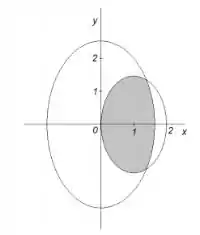
Como pode perceber, essa região é bem complicada para ser descrita, pois ela tem intersecções de duas elipses. Então, vamos pensar na região dividida em duas partes:

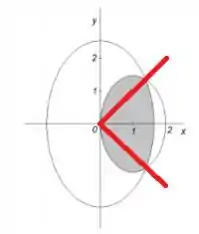
E veja ainda que a região é simétrica em relação ao eixo x , portanto podemos afirmar que área é duas vezes a área da parte de cima:

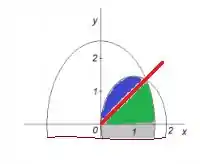
Em outras palavras, a área da região R é:

A R = 2 A v e r d e + A a z u l       →

A R = 2 ∬ v e r d e   1 d A + ∬ a z u l   1 d A

Então, basicamente, teremos calcular essas duas integrais e resolver o nosso problema! Vamos nessa?

Passo 2

Vamos começar descrevendo ambas as regiões!

Usando a dica do problema, vamos fazer isso usando uma mudança compatível com a maior elipse de equação:

2 x 2 + y 2 = 6

Passando essa equação para a equação geral da elipse:

2 x 2 + y 2 = 6       →

x 2 3 + y 2 6 = 1     →

x 2 3 2 + y 2 6 2 = 1

Assim, usando as Coordenadas de mudanças elípticas:

x = 3 ⋅ r cos ⁡ θ

y = 6 ⋅ r sin ⁡ θ

O Jacobiano dessa mudança é:

J = 3 ⋅ 6 ⋅ r       →

J = 3 2 r

Passo 3

Com isso, podemos descrever a região VERDE! (Lembre-se de que essa mudança faz o r variar da origem até a borda máxima, enquanto o θ varia do eixo x até o limite da região máximo):

Repare que:

0 ≤ r ≤ B o r d a   d a   e l i p s e   m a i o r

0 ≤ θ ≤ R e t a   v e r m e l h a

A borda da elipse maior tem equação:

x 2 3 2 + y 2 6 2 = 1

Substituindo as coordenadas elípticas acima:

x = 3 ⋅ r cos ⁡ θ             e             y = 6 ⋅ r sin ⁡ θ

x 2 3 2 + y 2 6 2 = 1             →                     3 2 ⋅ r 2 ⋅ cos 2 ⁡ θ 3 2 + 6 2 ⋅ r 2 ⋅ sin 2 ⁡ θ 6 2 = 1       →

r 2 ⋅ cos 2 ⁡ θ + r 2 ⋅ sin 2 ⁡ θ = 1           →               r 2 cos 2 ⁡ θ + sin 2 ⁡ θ = 1         →

r 2 = 1         →           r = 1

Logo:

0 ≤ r ≤ 1

0 ≤ θ ≤ R e t a   v e r m e l h a

Enquanto isso a reta vermelha: estamos falando da intersecção das duas elipses de equações...

2 x 2 + y 2 = 6   2 x 2 + y 2 = 4 x

Logo...

4 x = 6     →           x = 3 2

Como x = 3 ⋅ r cos ⁡ θ e r = 1 (pois estamos falando da intersecção da elipse maior com a menor):

3 ⋅ cos ⁡ θ = 3 2         →               cos ⁡ θ = 3 2 3 = 3 2

E agora eu te pergunto: qual o ângulo cujo cosseno é 3 2 ? Exato! 30 ° (ou π / 6 em radianos). Concluímos então que na região verde temos:

0 ≤ r ≤ 1

0 ≤ θ ≤ π 6

Passo 4

Agora podemos descrever a região azul!

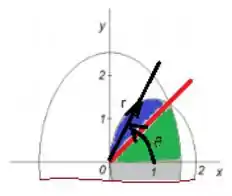
Temos aqui que a seguinte variação para r e θ :

0 ≤ r ≤ B o r d a   d a   e l i p s e   m e n o r

R e t a   V e r m e l h a ≤ θ ≤ π 2

Ora, a reta vermelha com essa mudança que fizemos lá no passo 2 tem ângulo de π / 6 . Portanto, só falta sabermos quem é a elipse menor nessas coordenadas. Assim como no passo, anterior, basta pegarmos a equação da elipse menor e substituir as coordenadas elípticas:

2 x 2 + y 2 = 4 x         →

2 3 2 ⋅ r 2 ⋅ cos 2 ⁡ θ + 6 2 ⋅ r 2 ⋅ sin 2 ⁡ θ = 4 3 ⋅ r cos ⁡ θ     →

6 ⋅ r 2 ⋅ cos 2 ⁡ θ + 6 ⋅ r 2 ⋅ sin 2 ⁡ θ = 4 3 ⋅ r cos ⁡ θ     →

6 ⋅ r 2 cos 2 ⁡ θ + sin 2 ⁡ θ = 4 3 ⋅ r cos ⁡ θ     →

6 ⋅ r 2 = 4 3 ⋅ r cos ⁡ θ     →

r = 2 3 3 cos ⁡ θ  

Então:

0 ≤ r ≤ 2 3 3 cos ⁡ θ

π 6 ≤ θ ≤ π 2

Passo 5

Prontinho, agora podemos remontar a integral que calcula a área da nossa região R :

A R = 2 ∬ v e r d e   1 d A + ∬ a z u l   1 d A

Como a região verde é:

0 ≤ r ≤ 1

0 ≤ θ ≤ π 6

Enquanto isso, a região azul é:

0 ≤ r ≤ 2 3 3 cos ⁡ θ

π 6 ≤ θ ≤ π 2

Logo:

A R = 2 ∫ 0 π 6 ∫ 0 1 1 ⋅ J   d r d θ + ∫ π 6 π 2 ∫ 0 2 3 3 cos ⁡ θ 1 ⋅ J   d r d θ       →

Como J = 3 2 r ...

A R = 2 ⋅ 3 2 ∫ 0 π 6 ∫ 0 1 r   d r d θ ⏟ I + ∫ π 6 π 2 ∫ 0 2 3 3 cos ⁡ θ r   d r d θ ⏟ I I  

Passo 6

Calculando a integral I :

∫ 0 π 6 ∫ 0 1 r   d r d θ =

∫ 0 π 6 ∫ 0 1 r   d r d θ = ∫ 0 π 6 r 2 2 0 1 d θ =

∫ 0 π 6 1 2 d θ = 1 2 θ 0 π 6 =

π 12

Passo 7

Calculando a integral I I :

∫ π 6 π 2 ∫ 0 2 3 3 cos ⁡ θ r   d r d θ =

∫ π 6 π 2 ∫ 0 2 3 3 cos ⁡ θ r   d r d θ = ∫ π 6 π 2 r 2 2 0 2 3 3 cos ⁡ θ d θ =

∫ π 6 π 2 2 3 3 cos ⁡ θ 2 2 d θ = ∫ π 6 π 2 4 3 cos 2 ⁡ θ 2 d θ =

2 3 ∫ π 6 π 2 cos 2 ⁡ θ d θ

Para calcular essa integral aí, lembre-se de que:

cos 2 ⁡ θ = 1 + cos ⁡ 2 θ 2

Então:

2 3 ∫ π 6 π 2 cos 2 ⁡ θ d θ = 2 3 ∫ π 6 π 2 1 + cos ⁡ 2 θ 2 d θ =

2 3 1 2 θ + sin ⁡ 2 θ 4 π 6 π 2 = 2 3 1 2 ⋅ π 2 + sin ⁡ π 4 - 1 2 ⋅ π 6 + sin ⁡ π 3 4 =

2 3 1 2 ⋅ π 2 - 1 2 ⋅ π 6 + 3 2 4 =

2 3 π 4 - π 12 - 3 8 = 2 3 π 6 - 3 8 = 2 π 18 - 2 3 24

Passo 8

Concluímos então que:

A R = 2 ⋅ 3 2 ∫ 0 π 6 ∫ 0 1 r   d r d θ ⏟ I + ∫ π 6 π 2 ∫ 0 2 3 3 cos ⁡ θ r   d r d θ ⏟ I I         →

A R = 6 2 π 12 + 2 π 18 - 2 3 24 =

6 2 π 12 + 12 2 π 18 - 12 6 24 =

2 π 2 + 2 2 π 3 - 6 2 =

7 2 π 6 - 6 2

Resposta

7 2 π 6 - 6 2

Exercícios de Livros Relacionados

Seja σ θ ,ρ = 2 ρ cos ⁡ θ ,ρ s e nθ . Mostre que σ transforma a reta ρ = 1 numa elipse. Desenhe tal elipse.
Calcule a área da região delimitada pela elipse
Seja σ a transformação do Exercício 10. Desenhe σ ( B ) onde B é o retângulo 0 ≤ ρ ≤ 1 , 0 ≤ θ ≤ 2 π .