Dois pêndulos, cada um composto por um fio de comprimento prendendo uma partícula de massa , realizam um movimento harmônico simples (pequenas amplitudes) com uma mola de constante elástica e massa desprezível unindo as massas no plano de oscilação. Quais o modos normais de oscilação?
- e
- e
- e
- e
- e
Passo 1
Bom , o sistema com que estamos lidando pode ser representado pela figura abaixo:
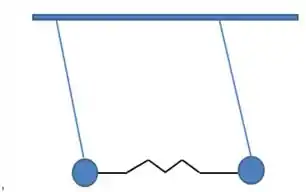
Podemos chamar de o deslocamento horizontal que a primeira massinha sofre, e de o ângulo que o pêndulo faz com a vertical. Da mesma forma, podemos chamar de e o deslocamento e o ângulo da massinha 2.Assim:
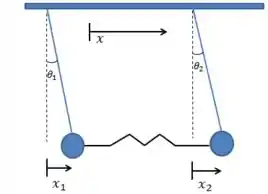
Estamos considerando ambos os deslocamentos positivos, como costumamos fazer.
Passo 2
Agora precisamos descobrir as forças que agem em cada bolinha. Vamos primeiro analisar as forças devido aos pêndulos.
Lembra como chegar na força que age num pêndulo simples? Nós costumamos decompor o peso na direção , o que gera:
Se não lembra bem, dá um pulinho lá no tipo de pêndulos simples.
Então as forças devido ao pêndulo simples serão do tipo escrito acima. Porém, temos também a força que a mola exerce em cada massa.
Vamos considerar que , com isso a mola estará sendo esticada, e a força que a mola exerce em cada massa terá o sentido abaixo:
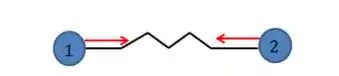
O módulo da força será dado por:
Passo 3
Seguindo o sentido que cada força tem, podemos escrever:
Para a massa 1:
Para a massa 2:
Bora usar agora a velha e boa aproximação para pequenos ângulos:
Assim:
Reorganizando as equações:
E temos o nosso sistema de EDO’s.
Passo 4
Agora vamos supor que as soluções são do tipo:
Substituindo nas equações e lembrando que:
Teremos:
Cortando todos os cossenos:
Isolando e
Passo 5
Agora vamos escrever o sistema na forma matricial:
Como não queremos a solução trivial ( o determinante da matriz acima tem que ser nulo. Assim:
Assim:
Então:
E:
Então a resposta é:
e)
Resposta
e)