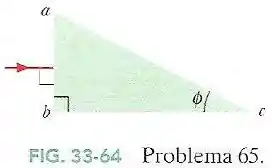
Na Fig.33-64 um raio luminoso incide perpendicularmente à face de um prisma de vidro ().
Determine o maior valor do ângulo para o qual um raio é totalmente refletido na face do prisma se este está imerso:
- No ar
- Na água (cujo índice de refração é )
Passo 1
Antes de partimos para resolver cada item, vamos observar a geometria do problema.
O raio luminoso vai entrar no prisma paralelamente ao lado , pois ambos o raio e esse lado são perpendiculares ao lado .
Por serem paralelos, o ângulo que o raio faz com o lado vai ser o mesmo, .
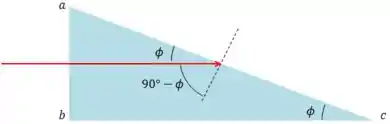
Isso significa que o ângulo de incidência é .
Passo 2
Letra a)
Seja o ângulo de incidência. Ele vai ser o ângulo crítico quando o ângulo de refração . Substituindo na lei de Snell:
Pelo enunciado e temos que lembrar que .
Tem uma relação trigonométrica que diz que:
Logo:
Passo 3
Letra b)
Quando estamos na água, a única coisa que muda em relação ao ar é o índice de refração do meio externo ao prisma. Fazemos então os mesmos passos.
Resposta
Letra a)
Letra b)