A ação combinada das três forças sobre a base em pode ser obtida estabelecendo sua resultante passando por Determine os módulos de e do momento associado.
Passo 1
Em outras palavras, o que o problema está te pedindo e o sistema força binário em
Vamos, primeiro, calcular a resultante das forças:
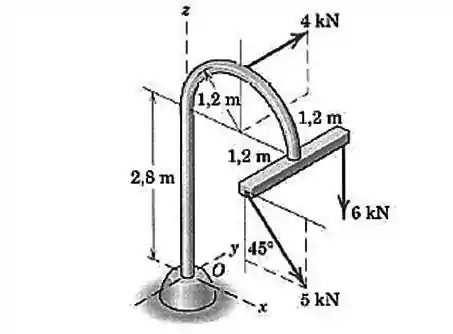
Temos uma força de que atua apenas na direção , uma força de que atua apenas na direção e uma de que atua no plano
Olhando o sentido positivo dos eixos na figura e escrevendo as forças em termos de vetores e:
Assim, o módulo de é dado por:
Passo 2
Agora vamos calcular o momento de cada uma das forças. Para isso, vamos ter que definir cada força e o vetor , ou seja, o vetor distância até
Vamos começar pela força de . Vamos chamá-la de :
O vetor é dado por:
A gente não precisa ficar subtraindo um ponto do outro sempre, já que é a origem. Basta a gente pegar o ponto de aplicação da força.
Perceba: tem um semicírculo ali no meio da figura, por isso que a distância em é:
Assim, o momento será dado por:
Passo 3
Agora vamos lidar com a força de . Ela é bem simples de ser definida, já que está apenas na direção
E o vetor Ele é bem parecido com o da força anterior, o que muda é a coordenada
Assim, o momento é dado por:
Calculando isso aí:
Passo 4
E por fim a última força, que pode ser definida facilmente também, essa por:
E o vetor posição? Esse será dado por:
Assim o momento será dado por:
Calculando:
Passo 5
Show agora é só somar todos os momentos:
Passo 6
Então podemos dizer que nosso sistema força-binário equivalente no ponto é representado pela força e pelos vetores abaixo: