Substitua as duas forças atuando no mastro por um torçor. Escreva na forma vetorial o momento associado com o torçor e especifique as coordenadas do ponto no plano pelo qual passa a linha de ação do torçor.
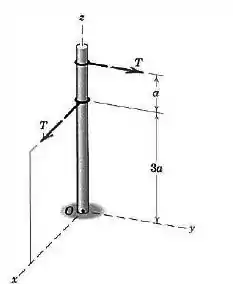
Passo 1
Primeiro vamos escrever a força resultante, observando a figura. Veja que existe uma força apontando na direção positiva de e outra no sentido positivo de
Assim, a força pode ser escrita como:
Passo 2
Agora vamos calcular o momento resultante. Para a força em
Assim:
Para a força em
Assim:
Passo 3
Escrevendo o momento do torçor como:
Passo 4
Usando a relação:
Queremos achar o ponto
Desenvolvendo
Calculando:
Assim:
Isso tudo igual a
Passo 5
Comparando termo a termo:
Da última equação:
Somando a primeira e a segunda:
Substituindo na primeira equação:
Passo 6
Assim, o ponto onde a linha de ação da força resultante passa é:
E o momento pode ser escrito como:
Observe que o sinal de menos na frente indica que o sentido do vetor momento é contrário ao sentido da força resultante.