Uma placa opaca tem algumas fendas igualmente espaçadas de uma distância de . A abertura de cada fenda é de . A placa é iluminada perpendicularmente por uma luz amarela com comprimento de onda . Em uma tela distante de da placa, a intensidade da luz é observada (ver figura).
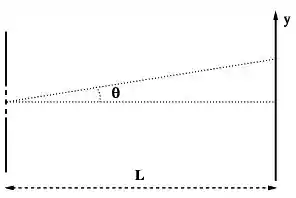
(a) Encontre a largura da envoltória central de difração formada na tela.
Passo 1
Mas o que o exercício quer?
O exercício quer que definamos o tamanho, ou seja, largura da envoltória central de difração, que é o ponto em que m=1, mas lembre-se que para fendas simples, a fórmula que nos dá os mínimos, e aqui vale uma observação, pois para interferência a fórmula dava máximos, mas para fendas simples ela nós dará mínimos e a fórmula é a seguinte.
Em que m=
Em que temos no nosso desenho o seguinte
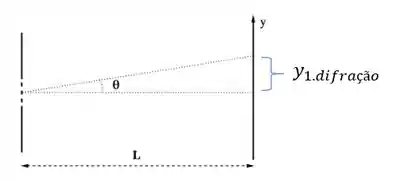
Passo 2
Olhando nossa figura vemos que
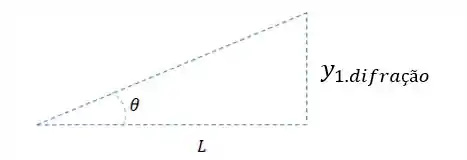
E pelo desenho que fizemos podemos considerar pelo triangulo que
Mas como faremos para achar o valor do ângulo?
Para isso basta que tomemos o valor de m=1 e analisemos a nossa equação principal
Logo
Isolando o seno teremos que
Passo 3
Temos pelo enunciado que
substituindo teremos que
Assim teremos que
Com o ângulo podemos substituir o valor na outra equação
Substituindo teremos que
Mas temos que tomar o seguinte cuidado, essa medida que fizemos contempla apenas o mínimo da parte de cima da interferência, porém ainda existe o mínimo da parte de baixo, ou nesse caso, quando m=-1, como existe simetria entre os mínimos, basta multiplicarmos o valor por 2, dessa forma teremos que