Considere a transformação linear definida por:
(a) Determine a matriz da transformação linear T na base canônica.
(b) Determine a equação cartesiana da imagem de T. Lembre que:
(c) Considere a base:
Determine a matriz da transformação linear T na base .
(d) Considere o plano de equação cartesiana:
Determine uma base da imagem de pela transformação T.
Passo 1
(a) Temos a base canônica do
Para achar a matriz que representa T na base , aplicamos T aos vetores da base e colocamos os resultados nas colunas de uma matriz.
Não esqueça que só podemos fazer isso direto pois estamos trabalhando com a base canônica!!
Então usando a fórmula dada no enunciado:
Logo:
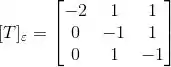
Passo 2
(b) A imagem de T é gerada pela transformação T aplicada aos vetores da base .
Vimos que:
Esses três vetores e não são paralelos entre si e geram a imagem de T.
Mas lembra lá da definição da transformação T:
Como esses vetores são resultados do produto vetorial entre algum vetor e o vetor , então todos são ortogonais ao vetor .
Então todos eles pertencem ao plano de equação:
Pois a equação geral do plano é , onde são as coordenadas de um vetor normal ao plano, e o nosso vetor normal é o
Por isso, a equação cartesiana da imagem de T:
Passo 3
(c) Para achar a matriz que representa T na base , aplicamos a transformação T aos vetores da base, escrevemos os resultados em coordenadas da base e só então colocamos essas coordenadas nas colunas de uma matriz.
Foi dado:
Podemos usar a definição de T dada no enunciado ou então multiplicar cada um desses vetores pela matriz que achamos no item (a)!
Fazendo do segundo jeito, para o vetor (1,1,1):
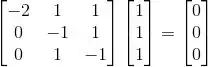
Esse vetor pode ser escrito como:
Logo:
Já para o vetor (1,-1,2):
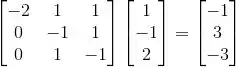
Agora queremos achar a,b e c tais que:
Pela segunda equação:
Substituindo na terceira:
Logo:
Substituindo esses valores na primeira equação:
Então achamos que:
Por último, vamos aplicar T ao vetor (6,0,0):
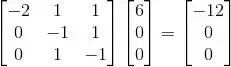
E as coordenadas do vetor (-12,0,0) na base são:
Portanto a matriz que representa T na base é:
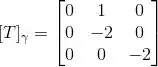
Passo 4
(d) Uma base para o plano pode ser dada por:
Calculando a imagem dos vetores da base:
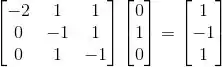
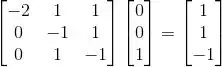
A imagem do plano vai ser então gerada por esses dois vetores e
Como os dois não são paralelos (um não é múltiplo escalar do outro), então eles formam uma base de
Resposta
(a)
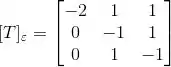
(b)
(c) 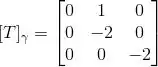
(d)