Uma partícula de massa encontra-se confinada em uma caixa unidimensional , descrita pela região .
A energia potencial é para pontos no interior da caixa e para pontos fora da caixa.
- Obtenha a expressão geral para os níveis quânticos de energia.
- Encontre as funções de onda normalizadas associadas a estes níveis.
- Ao diminuir-se o valor de , o que ocorre com a energia do estado fundamental? Discuta este fato de maneira breve, em termos puramente qualitativos.
- Qual é a probabilidade de se encontrar a partícula na região para o estado excitado do sistema?
Passo 1
Letra a)
Primeiro, vamos dividir a caixa em três regiões:
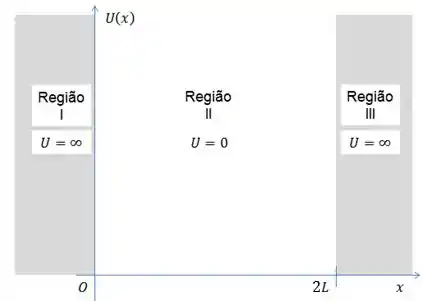
Vamos começar montando a equação de Schrödinger para cada uma delas.
Na Região e , o potencial é infinito, o que faz com que obrigatoriamente a função de onda se anule.
Na região , como , ficaremos com:
Rearrumando, temos:
A solução dessa equação diferencial é uma soma de funções trigonométricas!
Como a função de onda fora da caixa é zero, nas paredes da caixa a nossa função também tem que zerar. Isso nos diz duas coisas:
Para a segunda equação ser satisfeita, ou fazemos ,o que não é possível, pois nesse caso não teria função de onda (ela seria zero em todo lugar), ou .
O seno é sempre zero quando:
Rearrumando, isso nos diz como tem que ser!
Mas o nosso dependia da energia. Se ele é quantizado (pois ), a energia também vai ter que ser. Vamos igualar a condição do nosso com a definição dele.
Não se assuste se você viu uma fórmula onde o denominador era . A diferença entre elas é o tamanho da caixa: Em uma é e na outra é .
Passo 2
Letra b)
A função de onda dos níveis de energia vai ser:
Para normalizá-la, vamos integrar o seu quadrado em todo o eixo e igualar a (sendo que fora do intervalo de a , ela é nula).
Precisamos pegar emprestada uma relação da trigonometria, que diz o seguinte:
Substituindo:
Como , vamos ter que:
A função de onda normalizada então é:
Passo 3
Letra c)
A energia do estado fundamental corresponde a . Substituindo:
Ou seja, a energia do estado fundamental é inversamente proporcional ao quadrado de .
Se diminuir, também diminui, enquanto vai aumentar, aumentando a energia do estado fundamental.
Passo 4
Letra d)
A probabilidade de se encontrar a partícula no intervalo para o primeiro estado excitado () é dada pela seguinte integral:
Que é semelhante à que encontramos antes!
A probabilidade corresponde a !
Resposta
Letra a)
Letra b)
Letra c)
Se diminuir a energia do estado fundamental aumenta.
Letra d)