Seja uma partícula de massa confinada em uma região entre e no eixo .

a) Por substituição direta na equação de Schrodinger, mostre que a função de onda é uma solução possível para o estado dessa partícula e encontre o valor de sua energia.
b) A função de onda também é solução? Explique.
c) Se é sabido que a partícula se encontra em seu quinto estado de energia, esboce, em função de , a probabilidade de encontrar a partícula em uma posição qualquer.
d) Seja o caso dessa partícula ser o elétron e . Qual é o comprimento de onda do fóton emitido quando o elétron salta do quinto para o primeiro nível de energia?
Passo 1
Fala pessoal, prontos para uma questão de quântica?
O item (a) quer que verifiquemos se a função de onda
é solução da equação de Schrodinger. Para isso, vamos lembrar que da equação:
Nesse caso, no intervalo . Note que se trata de um problema do tipo posso quadrado infinito em que potencial é nulo dentro do intervalo e infinito fora. Assim, a equação fica
Para verificar se é solução dessa equação, basta derivar duas vezes com relação a :
Substituindo na equação, temos que
Logo, passando tudo para o mesmo lado
Com isso vemos que satisfaz a equação se o termo entre parênteses se anular:
Com isso, achamos de quebra a energia associada a essa partícula:
Passo 2
No item (b) ele pede para fazer o mesmo com a função
Derivando duas vezes com relação ao tempo, também achamos que
Logo, essa solução também satisfaz a equação! Porém será que é uma solução válida?
Note que na solução do item (a), temos que
Já para a função de onda do item (b):
Portanto, a função de onda não se anula na extremidade do poço infinito, que é uma condição necessária para uma solução da equação devido a condição de contorno que o potencial é infinito fora do intervalo. Portanto, a função apresentada no item (b) não é uma solução válida da equação de Schrodinger pois não satisfaz a condição de contorno no extremo do intervalo!
Passo 3
Para resolver os últimos dois itens, vamos achar a solução geral para esse problema. Você deve conhecer a solução geral para o poço quadrado infinito quando o intervalo é :
Se você quiser dar uma revisada de como se chega nessas fórmulas, dá uma olhada nos resumos do RespodeAí que você vai entender direitinho!
Acontece que no nosso problema, o intervalo do poço é . Note que a largura do poço é a mesma e igual a , porém a origem é diferente. Portanto, temos que fazer uma translação do sistema de coordenadas. Para isso, basta trocar por na expressão para :
Assim, o que antes acontecia na origem , agora acontece em e, o que antes ocorria em , agora ocorre em . Observe também que a energia não foi alterada por essa translação.
Observe também que a solução do item (a) corresponde a :
Usando :
Logo,
Trocando na energia:
Vemos que a energia também bate com o que achamos no item (a)!
Passo 4
Agora que temos a solução geral do problema, podemos resolver o item (c). Ele quer a distribuição de probabilidade para . Vamos olhar primeiro para a função de onda:
Por outro lado,
Como e , temos que
A função de probabilidade é o quadrado da função de onda:
A seguir eu ploto essa função no intervalo :
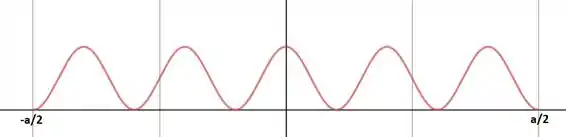
A função se anula em pontos no interior do intervalo (como deve ser) e esses pontos correspondem às posições em que é impossível encontrar a partícula (pontos nodais).
Passo 5
Bora para o item (d): quando o elétron salta do nível para o nível , ele libera uma energia
Essa energia é liberada na forma de um fóton, com energia
Assim,
Vamos lembrar que , de modo que
Logo,
Isolando :
Lembre-se que e para o elétron
Usando :
Com isso fechamos o problema 😉.
Resposta
não é uma solução válida pois não se anula nas extremidades do intervalo.