Seja uma base ortonormal do subespaço e seja , . Considere o vetor
(Aqui, denota o produto interno de e )
Pode-se afirmar que:
, onde denota a projeção ortogonal sobre .
é um conjunto ortogonal (mas não necessariamente ortonormal).
e são ortogonais.
.
Passo 1
A primeira coisa que você tem que perceber é que isso se parece MUITO com a fórmula de projeção em base ortogonal! Se liga:
Como nesse caso os vetores são ortonormais, temos que , então:
Agora substituindo as variáveis do problema:
Opa, então o vetor é definido como:
Isso já elimina a . Para as outras letras vamos fazer um desenho pra ficar mais claro:
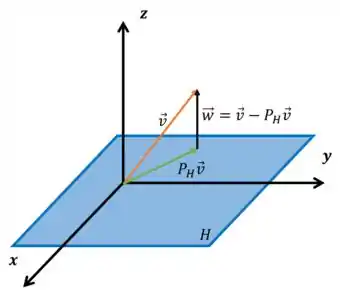
Usamos um plano pra ficar mais fácil de visualizar, mas sabemos que é um superplano de dimesão , já que sua base tem elementos. Nesse caso, vemos claramente que e não são ortogonais, e que não necessariamente é igual a !
Por outro lado, vemos que é perpendicular a ! Logo, é um conjunto ortogonal! Não podemos afirmar que é ortonormal pois, como vimos, não necessariamente é igual a . A letra é a correta.
Resposta
Letra