Questão 7: Seja
A série de Fourier da função , periódica de período , definida por
E seja sua soma. Podemos afirmar que:
- para todo .
- .
- apenas se .
- .
- para todo inteiro .
Passo 1
Pow, de acordo com o Teorema de Fourier, a gente pode afirmar que a soma é a função nos pontos do interior dos intervalos:
Logo a letra é falsa, pois não é a função , pois não é um ponto de interior e sim de extremo.
Passo 2
Pow, vamos verificar aqui a letra :
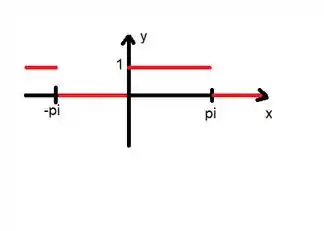
Pow, perceba que é um ponto extremo da função . Logo, por Fourier:
Como e o pela direita é :
Então aparentemente a letra está certa!
Passo 3
Mas vamos verificar os itens só pra ter certeza?
Pow, a letra está errada, pois já sabemos que:
Para verificar a e , temos que nos lembrar de que de acordo com Fourier:
Calculando então o já que (metade do período):
Mas tem duas definições nesse intervalo:
Então temos que separar a integral em duas partes:
Para calcular o ...
Separando a função em duas vertentes...
Agora integrando...
Como o cosseno de é ...
O o item também está errado!
Resposta
Alternativa