Suponha que a função dada é estendida, periodicamente, para fora do intervalo original.
- Encontre a série de Fourier da função estendida
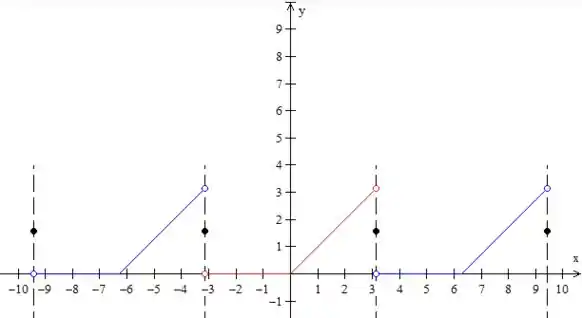
- Esboce o gráfico da função para qual a série converge por três períodos
Passo 1
Letra a)
Precisamos encontrar a Série de Fourier de , temos o seguinte:
Como o intervalo da função que o problema deu é (de até ) e temos que estender a função, esse será o seu período. Então:
Passo 2
Agora vamos calcular
Fazendo na expressão de temos:
Veja que de a temos duas expressões diferentes para , então o único jeito é dividir essa integral em duas, olha só:
Repare nos intervalos que escrevemos! A função vale em e em . Resolvendo essas integrais, temos
Passo 3
Agora vamos calcular os outros ’s. Temos que:
Dividindo essa integral, como fizemos com :
Agora vamos integrar por partes, ok? Fazendo
Agora vamos analisar com calma. Perceba que
Logo
Guarde isso!
Passo 4
Agora só falta calcular os ’s
Dividindo essa integral:
Agora vamos fazer a integração por partes:
Lembrando que
Temos
Passo 5
Agora vamos substituir tudo o que encontramos, temos:
Vamos separar a série em duas para ver melhor:
Agora vamos com calma. Não podemos escrever direto no somatório porque isso só vale para ímpar. Vamos definir então , porque isso garante que temos índices ímpares, ok? Para temos , portanto a série deve começar em .Temos então
Agora vamos substituir o valor de usando a notação também, só para ficar igual à primeira série
Já que as duas séries possuem os mesmos índices, podemos juntá-las, não é?
Passo 6
Letra b)
Certo, agora só falta o gráfico. Essa questão é bem simples, mas você tem que ter muito cuidado com a falta de atenção. O enunciado pede para desenharmos o gráfico da função para qual a série converge. Ah, é só desenhar a função do enunciado, né?
Não! O que você vai fazer nesse tipo de questão é o seguinte:
- Desenhar as informações sobre que o enunciado dá nos colchetes (em vermelho)
- Repetir essa para a esquerda e para a direita ignorando os pontos de descontinuidade (em azul);
- Fazer a média dos limites laterais em cada ponto de descontinuidade (em preto)
Porque isso? Por causa daquele Teorema da Convergência de Fourier que diz que a soma da série de Fourier de converge para onde a função é contínua (por isso nós copiamos essas retas do enunciado) e converge para a média dos limites laterais nos pontos de descontinuidade. Por exemplo, para , a soma da série converge para:
Lembre-se de fazer pontos preenchidos quando representar essas médias (em preto) e pontos “vazios” (em azul e vermelho) nos limites laterais.
Portanto, esse gráfico que fizemos não representa , mas a soma da sua série de Fourier, ok? Claro que a soma da série é muito parecida com a função.
Obs: Se a função periódica for toda contínua, a soma da série converge para em todos os pontos.