Seja
Sem calcular a série de Fourier (use o Teorema de Fourier), responda: para que valor a série de Fourier converge em ? (Não esqueça a justificativa.)
Calcule a séire de Fourier da função .
Tomando deduza o valor da soma
Passo 1
A função tem uma descontinuidade em , como mostra a figura abaixo.
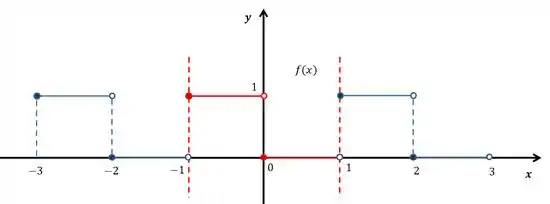
Pelo Teorema de Fourier, a série converge para o valor médio na descontinuidade. Assim:
Pela esquerda, tende a ; pela direita, tende a . Logo:
Então, a série converge para em .
Passo 2
Para calcular a série de Fourier, primeiro identificamos o período . Portanto, .
Assim, a série é dada por:
Passo 3
Vamos avaliar os coeficientes da série:
Note que as descontinuidades de não afetam a integral.
Agora, temos:
Passo 4
Para os coeficientes :
Mas note que
Então:
Passo 5
Assim, montamos nossa série:
Devido à particularidade de ser não-nulo somente para ímpar, escrevemos , e alteramos o somatório para :
Note que corresponde a , então o somatório em deve começar em também.
Finalmente, obtemos:
Passo 6
Vamos tomar, agora, .
Repara o seguinte: é sempre ímpar, de modo que o argumento do seno alterna entre e . Isto é, o seno alterna entre e .
Então o somatório vai ficar assim, olha:
Passo 7
Agora vamos dar uma rearrumada na equação:
Mas, sabemos que , portanto
Só trocar de para agora:
Resposta
.