Seja a função definida por
- Determine a série de Fourier de
- Esboce o gráfico da série de Fourier obtida no item (a) no intervalo [-6,6]
Passo 1
a)
Vamos lembrar das nossa fórmulas
Onde
Passo 2
Vamos calcular os coeficientes
Para
Como e
Passo 3
Vamos ao cálculo de .
Logo a nossa série será
Passo 4
b)
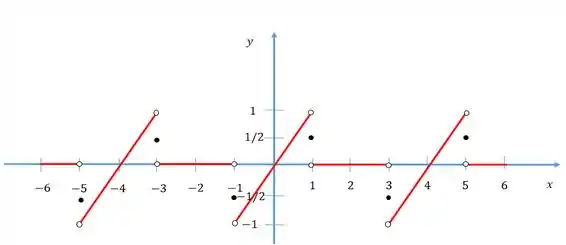
Para esboçar o gráfico dessa função no intervalo [-6,6] vamos ter que expandi-la.
Temos que definir valores novos para os pontos de descontinuidade de forma que
Assim teremos o gráfico abaixo.
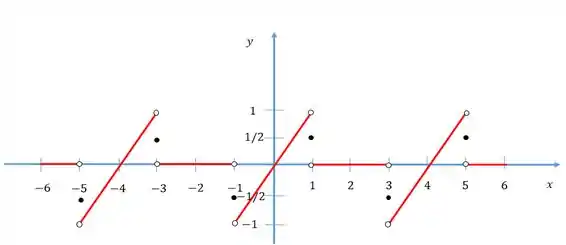
Resposta
a)
b)