A figura mostra um capacitor de placas paralelas com uma área das placas e uma distância entre as placas .
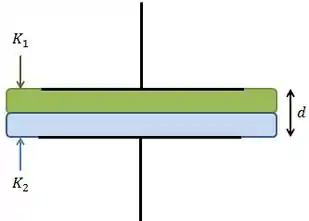
A metade superior do espaço entre as placas é preenchida por um material de constante dielétrica .
A metade inferior é preenchida por um material de constante dielétrica .
Qual é a capacitância?
Passo 1
Se observarmos bem, se uma corrente estivesse vindo de cima para baixo, por exemplo, ela passaria pelo dielétrico e depois pelo dielétrico , conseguiu visualizar?
Dá pra imaginar então que, ao invés desse troço complicado, nós poderíamos substituir isso por dois capacitores em série, um com o dielétrico e o outro com o dielétrico .
Uma forma diferente de resolver esse problema da forma apresentada na teoria é fazendo a soma das voltagens.
A voltagem resultante seria:
Sendo que, cada um desses “novos capacitores” teriam as placas separadas por .
Passo 2
A voltagem em cada um desses dielétricos é dada por:
Onde:
Sendo assim:
Agora é só jogar essa bagaça na equação que escrevemos no Passo 1.
Passo 3
Por último, vale lembrar que:
Arrumando isso aqui...
Agora sim! Só temos que fazer as contas.
Passo 4
Onde:
;
;
;
;
;
Logo: