Três placas condutoras de área são espaçadas de por vácuo (região ) e de por um material de constante dielétrica (região ), como indicado na figura. A carga total na placa superior é igual a , na placa do meio é igual a zero e na placa inferior é igual a . Desconsidere a não uniformidade do campo elétrico perto das bordas.
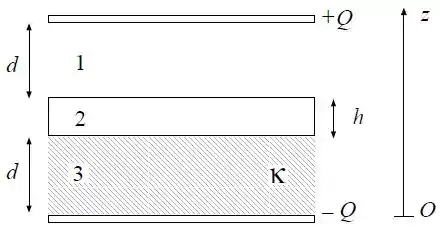
Indique numa figura e calcule as densidades de carga nas superfícies das placas condutoras. Calcule o vetor campo elétrico nas regiões e . Expresse suas respostas em termos de e.
Calcule a capacitância do sistema de três placas.
Calcule a densidade de carga de polarização no dielétrico.
Passo 1
Indique numa figura e calcule as densidades de carga nas superfícies das placas condutoras. Calcule o vetor campo elétrico nas regiões e . Expresse suas respostas em termos de e.
A densidade de carga na placa superior será:
Na placa inferior, que possui carga , a densidade de carga será:
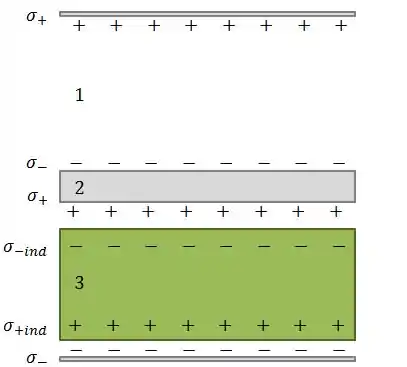
Como as placas são condutoras, para que a placa do meio possua carga neutra, por causa da indução das cargas nas placas superior e inferior, haverá um acúmulo de carga negativa na superfície superior da placa do meio e um acúmulo de cargas positivas na superfície inferior da placa do meio.
Assim, a superfície superior da placa do meio terá densidade de carga e a superfície inferior da placa do meio terá densidade de carga .
No final das contas, o capacitor vai ter essa cara:
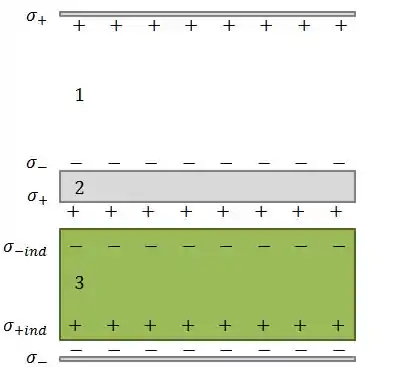
Como o problema pediu apenas a densidade de carga nas placas, não levamos em consideração a densidade de cargas induzidas que aparecerão no material dielétrico.
Passo 2
Agora temos que determinar o campo elétrico em cada uma das regiões.
- Região 1
- Região 2
- Região 3
O campo elétrico resultante está na direção vertical. Como há o acúmulo de cargas positivas na placa superior e negativas na superfície superior da placa do meio, o campo elétrico tem sentido de cima para baixo, logo:
Essa região corresponde ao interior do condutor, e aqui vai algo pra você guardar pra você no coração: O campo elétrico no interior de um condutor é sempre nulo.
Logo:
A única diferença desta para a região 1 é que, agora com o dielétrico, haverá uma variação do campo elétrico, que passará a ser dado por:
Essa mudança ocorre pois, em uma material dielétrico .
Passo 3
Calcule a capacitância do sistema de três placas.
Eu sei que pode parecer bizarro olhando assim, mas nós podemos dar uma simplificada nisso.
Ao invés de olhar para o capacitor como um sistema de três placas, podemos olhar pra isso como dois capacitores em série... o primeiro sem dielétrico e o segundo com o dielétrico.
Assim, a capacitância do sistema pode ser dada por:
Vamos chamar de a capacitância da parte sem o dielétrico. Como se tratam de placas planas e paralelas, dada por:
E de a capacitância da parte com o dielétrico:
Substituindo na fórmula da capacitância:
Passo 4
Calcule a densidade de carga de polarização no dielétrico.
O que ele tá chamando de carga de polarização aqui é o que nós chamamos de carga induzida lá no Passo 1.
No passo 2, escrevemos o campo elétrico na região 3 como:
Esse campo elétrico será a diferença entre o campo elétrico gerado pela densidade de carga (que estará de cima para baixo) e a densidade de carga (que está de baixo para cima). Logo:
Igualando as duas equações:
Todo mundo aqui está sendo dividido por , então podemos simplificar isso aqui:
Agora é só organizar isso:
Resposta