Um arranjo é formado por uma esfera condutora sólida de raio , centrada no ponto na origem, eletrizada com carga envolvida por um casca esférica condutora de raio interno e externo também eletrizada com carga , conforme ilustrado na figura abaixo:

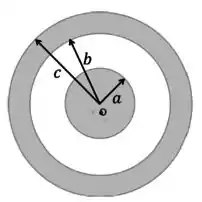
1. Sendo a distância até a origem , determine o vetor campo elétrico nas regiões ,, e .
2. Determine a carga em cada uma das superfícies , e na situação de equilíbrio eletrostático. Justifique sua resposta.
3. Determine as densidades superficiais de carga , e .

a) A primeira coisa que precisamos ver aqui é como as cargas se distribuem sobre as superfícies das esferas. Para isso, dá uma olhada na figura abaixo. Como a esfera de raio é condutora, a carga dela fica distribuída sobre a sua superfície. A presença dessa carga induz uma carga em na parte da casca esférica maior, como mostra a figura. Por isso, uma carga adicional vai para a superfície da esfera maior, deixando-a com carga .

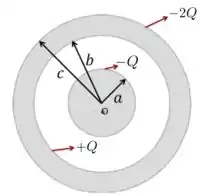
Agora que já sabemos como estão distribuídas as cargas sobre cada uma das cascas, vamos encontrar como é o módulo do campo elétrico em cada região. Nesse caso, precisamos nos lembrar de que ao fazermos uma superfície gaussiana, o campo elétrico sobre todos os pontos dessa gaussiana precisa ser o mesmo para utilizarmos a lei de Gauss. No caso do nosso problema aqui, que tem simetria esférica, podemos utilizar essa informação, além do fato de que o campo é sempre paralelo ao vetor   em todos o pontos da gaussiana.

Colocando tudo isso dentro da lei de Gauss, cuja superfície gaussiana é uma esfera de raio concêntrica, temos que

de forma que o vetor campo elétrico aponta na direção radial, especificada pelo versor  .

Pelo fato de o condutor estar em equilíbrio eletrostático, o campo dever ser nulo em seu interior e, portanto,   para . Todo excesso de carga deve estar na superfície do condutor.

Para , temos e, portanto,   ;

Para , o campo também deve ser nulo (interior do condutor) e, portanto,  .

Para , temos que e, portanto,  .