Exercícios de Lei de Gauss em Condutores - Lista de Exercícios Resolvida
Questão 1
Uma esfera condutora sólida de raio com carga está no interior de uma casca esférica muito fina isolante e concêntrica, com raio e que possui também uma carga . A carga está distribuída uniformemente sobre a casca esférica isolante. Dada essa situação e considerando que o sistema está no equilíbrio eletrostático, determine o módulo, direção e sentido do campo elétrico em cada uma das regiões , e .
Ver solução completaQuestão 2
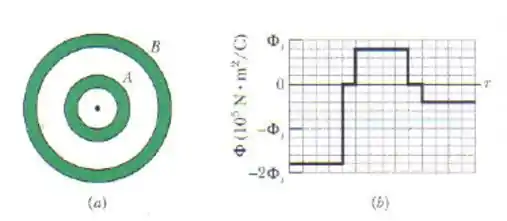
Uma partícula carregada é mantida no centro de duas cascas esféricas condutores concêntricas cuja seção reta aparece na figura. A figura mostra o fluxo através de uma esfera gaussiana com o centro na partícula em função do raio da esfera. A escala do eixo vertical é definida por . Determine:
(a) A carga da partícula central.
(b) A carga da casca
(c) A carga da casca
Questão 3
Os veículos espaciais que atravessam os cinturões de radiação da Terra podem interceptar um número significativo de elétrons. O acúmulo de cargas resultante pode danificar componentes eletrônicos e prejudicar o funcionamento de alguns circuitos. Suponha que um satélite esférico feito de metal com de diâmetro, acumule de carga.
(a) Determine a densidade superficial de carga do satélite
(b) Calcule o módulo do campo elétrico nas vizinhanças do satélite devido à carga superficial.
Ver solução completaQuestão 4
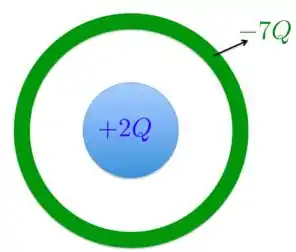
Considere a esfera sólida condutora e a casca esférica condutora concêntrica mostrada na Figura abaixo. A casca esférica tem carga . A esfera sólida tem carga .
- Quanta carga está na superfície interna da casca esférica?
- Considere, agora, que um fio metálico seja conectado entre a esfera sólida e a casca. Depois de o equilíbrio eletrostático ser restabelecido, quanta carga está na esfera sólida e em cada superfície da casca esférica? O campo elétrico na superfície da esfera sólida varia quando o fio é conectado? Se a resposta for positiva, de que maneira?
Questão 5
Uma pequena esfera oca condutora, com raio interno e raio externo , é concêntrica com uma grande esfera oca condutora, com raio interno e raio externo , como mostra a Figura abaixo. A carga total sobre a esfera oca interna é igual a e a carga total sobre a esfera oca externa é igual a . Considerando que o sistema está no equilíbrio eletrostático,
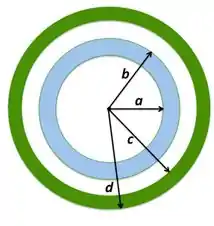
a) Determine o módulo, direção e sentido do campo elétrico em função de ao centro comum para as regiões
- ;
- ;
- ;
- ;
b) Qual é carga total sobre
- a superfície interna da esfera oca pequena;
- superfície externa da esfera oca pequena;
- a superfície interna da esfera oca grande;
- a superfície externa da esfera oca grande?
Questão 6
Um condutor esférico contém, em seu interior, uma cavidade esférica concêntrica. Uma partícula com carga encontra-se no centro da cavidade e o condutor, em equilíbrio eletrostático, possui carga elétrica total . Sendo o campo elétrico resultante em um ponto P fora do sistema, assinale o único item correto.
(a) ≠ e a carga total na superfície externa do condutor é zero.
(b) ≠ e a carga total na superfície externa do condutor é .
(c) = e a carga total na superfície externa do condutor é .
(d) = e a carga total na superfície externa do condutor é .
(e) = e a carga total na superfície externa do condutor é zero.
Questão 7
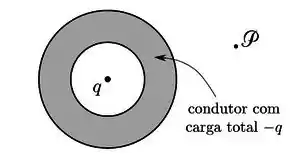
Um condutor isolado de forma arbitrária possui uma carga de . No interior do condutor existe uma cavidade; no interior da cavidade está uma carga pontual . Determine.
(a) A carga da superfície da cavidade.
(b) A carga da superfície externa do condutor.
Questão 8
O campo elétrico nas vizinhanças do tambor carregado de uma fotocopiadora tem um módulo de . Qual é a densidade superficial das cargas, supondo que o tambor é feito de um material condutor?
Ver solução completaQuestão 9
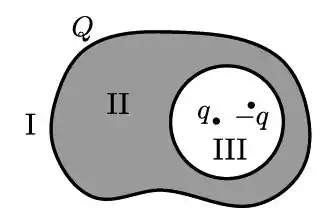
Um condutor, carregado com carga , possui uma cavidade esférica em seu interior. Nessa cavidade, há duas partículas, de cargas e . Chame de região o espaço fora do condutor, de região o condutor, e de região a cavidade. Qual das opções à seguir descreve corretamente o comportamento do campo elétrico nas três regiões?
Questão 10
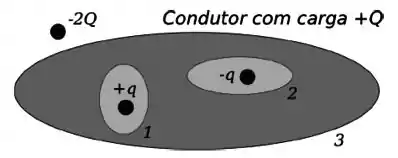
Considere um material condutor com carga positiva com duas cavidades em seu interior, conforme figura. Na cavidade 1 existe uma carga positiva . Na cavidade 2 existe uma carga negativa . Fora do condutor, temos ainda uma carga negativa . A carga total no condutor está distribuída de acordo com:
- na superfície 1; na superfície 2; na superfície 3.
- na superfície 1; na superfície 2; na superfície 3.
- na superfície 1; na superfície 2; na superfície 3.
- na superfície 1; na superfície 2; na superfície 3.
- nas três superfícies.
Questão 11
9ª questão - Considere 3 esferas condutoras idênticas de raio . A primeira esfera, eletricamente neutra, é posta em contato elétrico com a segunda, com carga . Em seguida, é posta em contato elétrico com a terceira esfera, cuja carga vale . O campo elétrico produzido pela primeira esfera a uma distância de seu centro vale:
A) , apontando para fora da esfera
B) , apontando para dentro da esfera
C) , apontando para fora da esfera
D) , apontando para dentro da esfera
E) zero
Ver solução completaQuestão 12
Uma esfera isolante maciça de raio está carregada com uma carga . Ela é circundada por uma casca esférica concêntrica, condutora, de raio interno e raio externo , que está carregada com uma carga .
Assinale a opção que especifica as cargas na superfície interna de raio e na superfície externa de raio .
- ,
- ,
- ,
- ,
- ,
Questão 13
Um arranjo é formado por uma esfera condutora sólida de raio , centrada no ponto na origem, eletrizada com carga envolvida por um casca esférica condutora de raio interno e externo também eletrizada com carga , conforme ilustrado na figura abaixo:
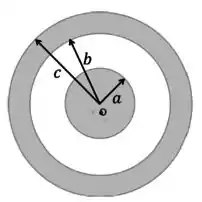
- Sendo a distância até a origem , determine o vetor campo elétrico nas regiões ,, e .
- Determine a carga em cada uma das superfícies , e na situação de equilíbrio eletrostático. Justifique sua resposta.
- Determine as densidades superficiais de carga , e .
Questão 14
O campo elétrico produzido por uma distribuição esfericamente simétrica de cargas tem a forma , onde é a distância até a origem de um sistema de coordenadas, que coincide com o centro da distribuição, e é o vetor unitário da direção radial. O gráfico é mostrado na figura abaixo. Considere que a distribuição se encontra em equilíbrio eletrostático, que e que .
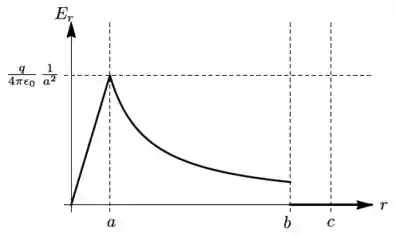
Sobre essa distribuição, considere as seguintes afirmativas abaixo:
- A região está preenchida por um material isolante uniformemente carregado.
- A região está preenchida por um material condutor perfeito.
- A carga total contida na região é nula.
São VERDADEIRAS as seguintes afirmativas:
- e
- e
- e
- , e
- Nenhuma delas.
Questão 15
15 - Uma esfera isolante maciça de raio encontra-se uniformemente carregada com uma densidade volumétrica de carga . Ela está envolvida, sem contato elétrico, por uma casca esférica condutora, com uma carga total e raio interno e raio externo (), como mostrado na figura abaixo. A esfera e a casca são concêntricas e o sistema se encontra em equilíbrio eletrostático. O módulo do campo elétrico produzido pelo sistema dentro da casca condutora vale.
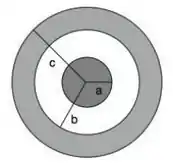
- Zero
Questão 16
(Capítulo 23 – Problemas Adicionais – Exercício 65) Uma carga Q está distribuída uniformemente em uma esfera de raio R. (a) Que fração da carga está contida em uma esfera de raio r = R/2,00? (b) Qual é a razão entre o módulo do campo elétrico no ponto r = R/2,00 e o campo elétrico na superfície da esfera?
Ver solução completaQuestão 17
(Capítulo 23.6 – Exercício 17) Uma esfera condutora uniformemente carregada com de diâmetro possui uma densidade superficial de cargas . (a) Determine a carga da esfera. (b) Determine o fluxo elétrico através da superfície da esfera.
Ver solução completaQuestão 18
7 - Uma carga pontual Q é posicionada dentro de uma casca esférica metálica neutra, conforme indicado na figura. O vetor campo elétrico no ponto P é dado por:
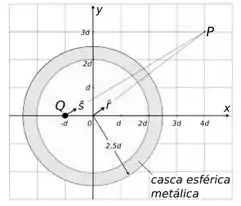
Questão 19
Um condutor possui duas cavidades separadas. No interior de uma cavidade há uma partícula de carga () e no interior da outra cavidade há uma partícula de carga . Sabendo que o condutor está neutro e que o sistema se encontra em equilíbrio eletrostático, podemos afirmar que a carga total distribuída sobre a superfície externa do condutor vale:
- 0
Questão 20
Considere a seguinte experiência: “Um cientista construiu uma grande gaiola metálica, isolou-a da Terra e entrou nela. Seu ajudante, então, eletrizou a gaiola, transferindo-lhe grande carga.” Pode-se afirmar que:
- O cientista nada sofreu, pois o campo elétrico era maior no interior que na superfície da gaiola.
- Mesmo que o cientista houvesse tocado no solo, nada sofreria, pois o potencial de seu corpo era o mesmo que o do solo
- O cientista nada sofreu, pois o potencial da gaiola era menor que o do seu corpo
- O cientista levou choque e provou com isso a experiência da corrente elétrica
- O cientista nada sofreu, pois o potencial de seu corpo era o mesmo que o da gaiola
Questão 21
Uma carga puntiforme está no centro de uma camada esférica condutora de raio interno e raio externo . A uma distância da carga, o campo elétrico tem módulo e aponta radialmente para fora. A uma distância da carga, o campo elétrico tem módulo e aponta radialmente para dentro da camada. Determine em função de , , , , , e :
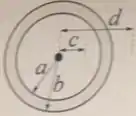
a) O valor e o sinal da carga puntiforme.
b) O sinal e o valor da carga na superfície externa da camada condutora.
Ver solução completaQuestão 22
Uma grande camada esférica metálica está inicialmente descarregada. Ela está apoiada sobre um suporte isolante e tem um pequeno orifício na parte superior. Uma pequena tachinha metálica carregada com carga é baixada por um fio de seda através do orifício, até tocar o interior da camada. Qual é a carga da superfície externa da camada?
- ;
- ;
- 0 ;
- ;
- .
Questão 23
Uma partícula de carga é colocada do lado de fora de uma grande camada esférica condutora neutra. Em qualquer ponto do interior da camada, o campo elétrico produzido pelas cargas superficiais da camada aponta:
a) para a carga .
b) para a superfície.
c) para longe da carga .
d) para longe da superfície
e) nenhuma das alternativas.
Ver solução completaQuestão 24
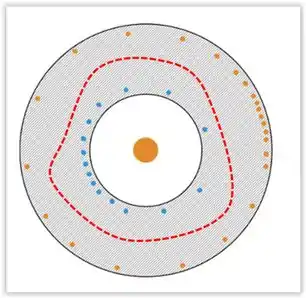
Considere o corte plano de um condutor, em equilíbrio eletrostático, com fronteira , conforme mostrado na figura abaixo; a parte sombreada representa o interior do condutor.
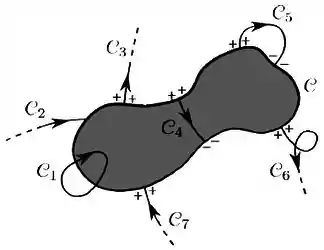
Das curvas , , todas no próprio plano de corte da figura, qual(is), nitidamente, não pode(m) representar linha(s) de campo elétrico?
e .
e .
e .
e .
.
Ver solução completaQuestão 25
Sobre um condutor maciço em equilíbrio eletrostático, considere as afirmativas abaixo:
- Se o condutor está carregado, sua superfície deve possuir um potencial elétrico diferente de seu interior.
- O campo elétrico é sempre tangente à superfície do condutor na vizinhança externa do mesmo.
- No interior do condutor, o campo elétrico deve ser necessariamente nulo.
São VERDADEIRAS as afirmativas:
- I
- II
- III
- I e II
- I e III
- II e III
- I, II e III
- Nenhuma delas.
Questão 26
Duas cascas esféricas condutoras concêntricas e , têm a disposição indicada na figura abaixo. A casca tem raio interno , raio externo e está carregada com uma carga líquida . A casca tem raio interno , raio externo e está carregada com uma carga líquida desconhecida .
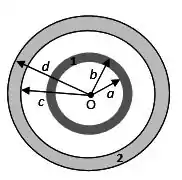
Medidas realizadas no sistema mostram que:
- o fluxo elétrico através de uma superfície gaussiana esférica de raio é igual a
- a densidade de carga na superfície externa da casca é igual a .
Com estas informações responda aos itens abaixo:
(a) Qual é o valor da carga líquida na casca ?
(b) Encontre o campo elétrico nas regiões e .
(c) Desenhe as cascas concêntricas e calcule (indicando também no desenho) as distribuições de carga nas superfícies internas e externas das duas cascas esféricas.
(d) Considere agora que no centro do sistema das cascas (ponto ) seja colocada uma carga puntiforme negativa de valor . Calcule o novo valor da densidade de carga na superfície externa da casca .
Ver solução completaQuestão 27
Duas esferas condutoras idênticas, muito pequenas, estão separadas por uma certa distância Originalmente, as duas esferas têm cargas de mesmo módulo e sinais opostos, e o módulo da força entre elas é , mantendo-se a distância, metade da carga de uma esfera é então movida para outra. O módulo da nova força entre as esferas é:
Questão 28
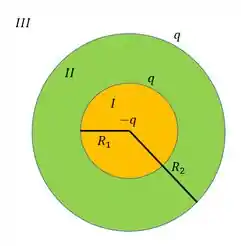
Uma esfera isolante maciça de raio está carregada com uma carga . Ela é circundada por uma casca esférica concêntrica, condutora, de raio interno e raio externo , que está carregada com uma carga de modo que a quantidade de carga na superfície interna é e na superfície externa é também.
Assinale a opção que especifica, corretamente o módulo dos campos elétricos nas regiões (), () e ()
- ; ;
- ; ;
- ; ;
- ; ;
- ; ;