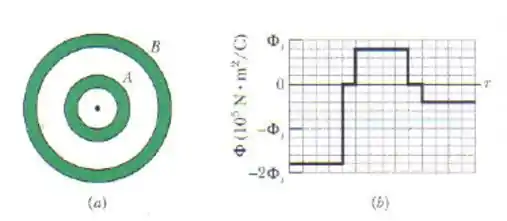
Uma partícula carregada é mantida no centro de duas cascas esféricas condutores concêntricas cuja seção reta aparece na figura. A figura mostra o fluxo através de uma esfera gaussiana com o centro na partícula em função do raio da esfera. A escala do eixo vertical é definida por . Determine:
(a) A carga da partícula central.
(b) A carga da casca
(c) A carga da casca
Passo 1
Para os raio menores, o fluxo elétrico se encontra estabilizado em . Esses fluxos são aqueles gerados pelas menores gaussianas possíveis: aquelas que estão dentro da casca esférica .
Como essas gaussianas possuem apenas a carga central dentro delas, podemos utilizar com essa informação a lei de Gauss no caso em que
Atenção: olhando o gráfico, vemos que cada escala vale pois ocorre uma variação de a cada escalas.
Isolando a carga:
Passo 2
Quando aumentamos o raio aos poucos, durante um trecho pequeno o fluxo fica igual a . Aqui a gente precisa interpretar. Isso acontece quando a distância está dentro da casca esférica ou dentro da casca esférica .
Nesses casos, o efeito blindagem do metal impede que existam campos elétricos no interior dele e isso acontece porque todas as cargas correm para a superfície numa disposição que zera o campo elétrico dentro das cascas.
Se a carga de dentro valer , a carga induzida na superfície interior da casca vale como já vimos na parte de indução eletroestática.
O campo dentro da casca precisa ser nulo porque, se não fosse, haveria cargas se movendo no interior da casca, e isso não acontece pois as únicas cargas que encontramos se encontram na parte superficial do metal!
Passo 3
Quando o raio se encontra entre a menor e a maior casca esférica, o valor de precisa incluir tanto a carga de quanto a carga que está no centro das duas cascas. Por isso, esse tipo de problema tem que ser resolvido de dentro para fora.
Dessa forma a gente consegue encontrar o valor das cargas em cada passo de maneira mais rápida!
Nesse caso:
Passo 4
Depois de aumentar um raio mais um pouquinho, enquanto o raio se encontra dentro da casca esférica , o fluxo continua dando e a razão é a mesma: o efeito blindagem – o campo elétrico no interior de metais condutores é sempre nulo no equilíbrio.
Agora, quando saímos da segunda casca esférica e chegamos à região mais à direita do gráfico, o fluxo se estabiliza em . Quando aplicarmos o teorema de Gauss agora, devemos incluis as três cargas: das duas cascas e da carga puntiforme lá de dentro. Então:
Passo 5
Só falta agora substituir e correr pro abraço!
Resposta
(a)
(b)
(c)