Um condutor isolado de forma arbitrária possui uma carga de . No interior do condutor existe uma cavidade; no interior da cavidade está uma carga pontual . Determine.
(a) A carga da superfície da cavidade.
(b) A carga da superfície externa do condutor.
Passo 1
Também se fala sobre esse tipo de questão lá em indução eletroestática, onde nós apresentamos o efeito blindagem. O lance é que ele também pode ser deduzido por meio da lei de Gauss.
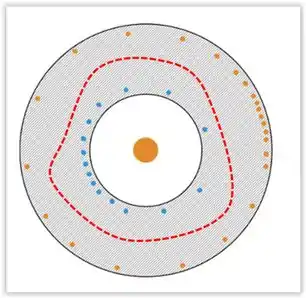
Olha essa gaussiana vermelha, bem no interior do condutor. Como não pode existir campo elétrico nesse interior, o fluxo na gaussiana vermelha é zero. Logo:
Passo 2
Mas é a soma entre as cargas azuis, induzidas no interior da casca e a carga puntiforme dentro da casca. Logo:
Passo 3
Como não as cargas não podem ficar no interior do condutor quando este alcança o equilíbrio eletroestático, todo o resto das cargas pulam para fora. Pela conservação das cargas:
Resposta
(Carga da superfície da cavidade)
(Carga da superfície externa do condutor)