UFJF – Física 3 – AV2 – Questão 2a
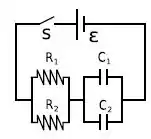
Uma bateria ideal de força eletromotriz está conectada a um circuito composto de dois
resistores e dois capacitores, como mostra o esquema da figura. Inicialmente, a chave S está aberta e os capacitores estão completamente descarregados. Sabe-se que e que .
- A chave S é fechada em . Calcule a corrente que passa pelo circuito em função de
Passo 1
Olá, tudo tranquilo? Bora resolver essa questão?
A ideia aqui é calcular a corrente que passa pelo circuito em função de . E por que eu destaquei o circuito? Porque antes de mais nada, precisamos achar a constante de tempo, já que esse é um circuito com resistores e capacitores!
Com esse tempo, vamos ser capazes de calcular a quantidade de carga nos capacitores, lembrando que se trata de um circuito que está inicialmente com os capacitores descarregados
E por fim, com a carga, é só derivar para achar a corrente!
Mas pode ficar tranquilo, vou fazer passo a passo com você!
Vamos começar?
Passo 2
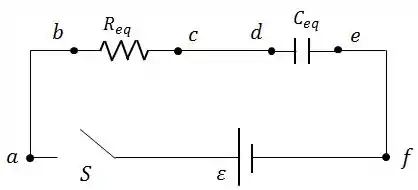
Antes de começar o problema aqui, a primeira coisa que devemos fazer é simplificar esse circuito.
Temos duas resistências em paralelo, de modo que a resistência equivalente será:
Da mesma forma, temos dois capacitores em paralelo, de forma que a capacitância equivalente será:
Assim, o circuito, que antes tinha uma cara escrota, agora ainda tem uma cara ainda escrota, mas um pouco melhor...
Quando o capacitor está inicialmente descarregado, a equação que determina o seu carregamento, é dada por:
Onde o produto é chamado de constante de tempo capacitiva.
Logo:
vamos substituir os dados?
Sabe-se que e que , assim
Passo 3
No passo anterior falamos um pouco de como a carga varia em função do tempo durante o carregamento, certo?
Então, se queremos descobrir a corrente, a única coisa que temos que fazer aqui é derivar a expressão:
Logo:
Substituindo aqui a expressões de e (usando e que , assim)
Mas antes de sair arrumando expoentes, vamos nos atentar que nesse item o problema pede a corrente no instante inicial, quando :
Ufa! Terminamos! Bora para o segundo item?