Seja .
Verifique que possui um zero no intervalo ;
Justifique teoricamente o comportamento da sequência colocada a seguir, gerada pelo método de Newton para o cálculo do zero de em , com e precisão .
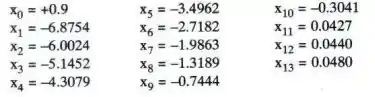
Passo 1
Vamos verificar pelo Teorema de Bolzano:
Como temos , então existe uma raiz nesse intervalo.
Passo 2
-
Repare que a sequência começa divergindo e depois passa a convergir para a raiz. Uma explicação para esse comportamento seria se , explodindo o quociente da nossa função de iteração. Testando isso:
Que é um valor próximo de , daí o comportamento estranho da sequência.
Resposta
Ei, a resposta está no passo a passo :)