Assinale a alternativa INCORRETA:
(a) De acordo com o Princípio de Pascal, uma variação de pressão aplicada a um fluido incompressível contido em um recipiente é transmitida integralmente a todas as partes do fluido e às paredes do recipiente;
(b) Dado que um objeto de madeira flutua em um fluido, a força de empuxo atuando sobre o objeto é maior que o peso do objeto. Isso ocorre porque a densidade do fluido é maior que a densidade do objeto em questão;
(c) Os fluidos são gases ou líquidos;
(d) A pressão _e uma medida da força por unidade de àrea exercida por um fluido;
(e) Um fluido ideal é incompressível, ou seja, sua massa específica tem um valor uniforme e constante;
(f) Se a velocidade de um fluido aumenta enquanto o fluido se move horizontalmente ao longo de uma linha de fluxo, a pressão do fluido aumenta.
Passo 1
a) Verdadeiro: Considere a pressão em qualquer ponto de um líquido nas configurações da figura abaixo:
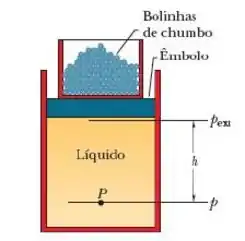
Neste caso:
Aumentando o número de esferas no recipiente sobre o êmbolo, aumentamos a pressão externa. Quando tratamos de pequenas variações da pressão podemos considerar que a equação acima se torna uma expressão do tipo:
Logo, vemos que a variação de pressão externa independe da altura, de modo que a pressão varia igualmente em todos os pontos do fluido.
Passo 2
b) Verdadeiro. Sabemos que:
com sendo o empuxo e a massa de fluido deslocado.
Se o fluido tem densidade :
,
onde o volume do objeto submerso no fluido é , onde e são a massa e a densidade do objeto. Logo, substituindo na equação, temos que:
se
Passo 3
c) Verdadeiro. Um fluido é definido como qualquer substância que pode escoar, ou seja, líquidos ou gases;
Passo 4
Passo 5
d) Verdadeiro. A definição de pressão é:
Onde F é perpendicular à área de aplicação da força.
Passo 6
e) Verdadeiro. O escoamento de um fluido ideal precisa ser incompressível para sua massa específica em todos os pontos ser constante.
Passo 7
f) Falso. Da equação de Bernoulli sabemos que:
Resposta
Letra f