Na figura abaixo, uma mola de constante elástica liga uma viga rígida ao êmbolo de saída de um macaco hidráulico. Um recipiente vazio de massa desprezível está sobre o êmbolo de entrada. O êmbolo de entrada tem uma área e o êmbolo de saída tem uma área 18,0A. Inicialmente, a mola está relaxada. Quantos quilogramas de areia devem ser despejados (lentamente) no recipiente para que a mola sofra uma compressão de ?
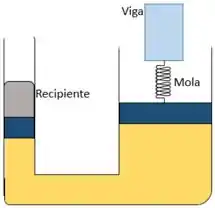
Passo 1
Pelo princípio de Pascal, nós temos que:
Passo 2
Aqui vai uma observação: a força exercida sobre o êmbulo maior é justamente a força elástica () pela mola e a força exercida sobre o êmbulo menor será a força peso (), à medida que o recipiente for preenchido. Então:
Onde é a deformação da mola e vale , e . Com isso:
Passo 3
Resposta
Devem ser despejados de areia.