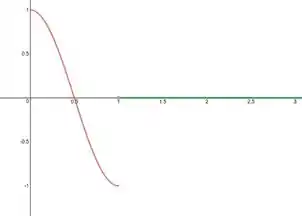
- Esboce o gráfico da seguinte função no intervalo
- Determine a transformada de Laplace da função do item (a).
Passo 1
Começamos com a letra (a). Bem, a primeira coisa a fazer é o traçado da função cosseno de até . A função é sempre senoidal, mas vamos determinar uns pontos para nos ajudar:
Ok, já temos uma base boa. Tracejando:
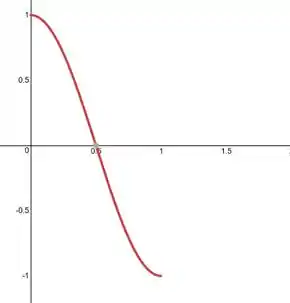
Para a função vale zero, então traçamos a constante zero:
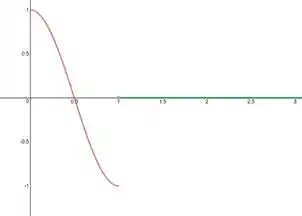
E tá feito nosso gráfico.
Passo 2
Agora vamos para a letra (b). Legal, como temos uma função definida por partes, vamos tentar representá-la por meio de funções degrau.
A função seguia livremente até que desaparece em . Isso significa que tem um degrau multiplicando a mesma função que subtrai e começa em :
Vamos agora determinar a transformada dessa função. Aplicando a transformada, temos:
Usando as propriedades da transformada:
Vamos olhar para cada transformada. Por tabela, temos que:
Assim, comparando temos e, portanto:
OK. Agora vamos para:
Temos que:
Comparando, . Então:
Então:
Então:
Agora vamos abrir esse cosseno:
Juntando tudo: