Quando dois vetores e são desenhados a partir de um mesmo ponto, o ângulo entre eles é .
- Usando técnicas vetoriais, mostre que o módulo da soma destes vetores é dado por
- Se e possuem o mesmo módulo, qual deve ser o valor de para que o módulo da soma de vetores seja igual ao módulo de ou de ?
Passo 1
A gente tem aqui que mostrar que a soma de dois vetores que saiam do mesmo ponto tenham módulo dado pela equação mostrada. Antes de mais nada vamos relembrar o que é o módulo da soma de dois vetores, se liga no desenho:
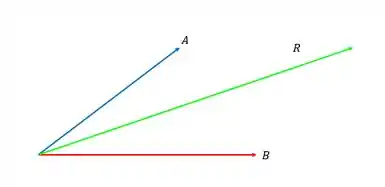
A resultante é a soma dos dois vetores que partem do mesmo ponto, então o seu comprimento é o módulo desse vetor e é ele quem queremos mostrar que é dado pela equação.
Se lembra os modos que a gente aprendeu pra somar dois vetores? Então, essa fórmula ai é muito parecida com a lei dos cossenos, né?
Então elas devem ter algo a ver.

A diferença ta no sinal do ), né? Isso é porque esse ângulo se for comparado ao ângulo que deve ser usado na lei dos cossenos tem o mesmo valor do cosseno só que com o sinal invertido! Se liga só!

Na lei dos cossenos usamos o ângulo , mas podemos usar aplicando a seguinte relação:
Assim, quando eu substituir isso na equação das leis dos cossenos o ultimo termo fica positivo!!!
Passo 2
Letra b) Aqui é o seguinte precisamos encontrar o ângulo entre vetores iguais que façam com que o módulo da soma tenha o mesmo módulo de um dos vetores que são iguais. Então comecemos aqui igualando esses camaradas, já que é o que o enunciado nos fala.
Como ele fala que o módulo resultante da soma é o módulo de ou , podemos substituir na equação.
Assim temos:
Assim temos: