Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Caso Escalar R³

Ver Teoria
Exercício 241234567891011121314151617181920212223252627282930313233343536373839404142434445464748

Enunciado

Questão 1: Considere a superfície parametrizada r t ,   θ = t cos ⁡ θ ,   t sin ⁡ θ ,   t 3 ,     t ∈ 1 ,   2 ,     θ ∈ 0 ,   2 π , cuja imagem denotaremos por S .

a) Calcule uma equação implícita para S .

b) Faça um esboço de S .

c) S é uma superfície parametrizada regular ou não? Justifique a resposta.

d) Calcule a equação implícita do plano tangente a S no ponto r 2 ,   π .

e) Calcule a integral de superfície ∬ S   x 2   d S .

Passo 1

a )

Então, vamos sempre começar problemas como esse, de passar da parametrização para a equação implícita, retirando algumas informações da própria equação paramétrica...

r t ,   θ = t cos ⁡ θ ,   t sin ⁡ θ ,   t 3

Então...

x = t cos ⁡ θ

y = t sin ⁡ θ

z = t 3

Sacou? Então o que precisamos fazer basicamente é chegar numa expressão envolvendo apenas x , y e z . Bora lá!

Passo 2

Como o x e o y envolvem cosseno e seno, se elevarmos ao quadrado e somar...

x 2 = t 2 cos 2 ⁡ θ

y 2 = t 2 sin 2 ⁡ θ

somando...

x 2 + y 2 = t 2 cos 2 ⁡ θ + t 2 sin 2 ⁡ θ     ⇒

x 2 + y 2 = t 2 cos 2 ⁡ θ + sin 2 ⁡ θ       ⇒

Como o cos 2 ⁡ θ + sin 2 ⁡ θ = 1 ...

x 2 + y 2 = t 2

Viu como é interessante fazer isso? Você simplesmente desaparece com o termo θ dali !

Passo 3

Como z = t 3 e ainda não usamos essa informação...

z = t 3         ⇒             t = z 3

Substituindo na equação que encontramos...

x 2 + y 2 = t 2         ⇒         z 3 2 = x 2 + y 2           ⇒

z 2 3 = x 2 + y 2

Prontinho! Eis aí uma equação implícita para a superfície pedida !

Passo 4

b )

Para esboçar a superfície S , vamos com calma. Vamos começar vendo qual é a cara da curva de intersecção da superfície S , com o plano y = 0 ... Se pegarmos a equação implícita que acabamos de definir...

z 3 2 = x 2 + y 2                 ⇒       c o m   y = 0       ⇒

z 3 2 = x 2

Extraindo a raiz...

z 3 = x             ⇒

Elevando ao 3 ...

z = x 3

Epa! Chagamos uma equação conhecida. A equação de uma curva cúbica...

Mas, não queremos essa curva toda, afinal sabemos que t ∈ 1 ,   2 ...

z = t 3       →           z = 1 3 = 1

z = t 3       →           z = 2 3 = 8

Então queremos apenas o pedacinho que vai de z = 1 a z = 8 ... Bem, essa é a cara da curva de intersecção da superfície no plano y = 0 . Mas o que acontece na intersecção com o plano x = 0 ?

Passo 5

Como a equação é...

z 3 2 = x 2 + y 2                 ⇒       c o m   x = 0       ⇒

z 3 2 = y 2

Já calculamos isso aí, e vamos chegar a...

z = y 3

Com z indo de 1 a 8 ...

Repare que a curva foi à mesma, nó apenas giramos em torno do z , o que nos sugere que a superfície S , vai ser a rotação dessa curva ao redor do eixo z ... Esse negócio de sugere não é legal, neh? É bom nós termos certeza, e cara, vou te contar um segredinho que talvez você já até sabe: essa parametrização aqui:

r t ,   θ = t cos ⁡ θ ,   t sin ⁡ θ ,   t 3

Por ter cos ⁡ θ e sin ⁡ θ em x e y , caracteriza uma superfície de revolução ao redor de z , portanto estamos corretos ao dizer que a superfície foi essa que encontramos por lógica:

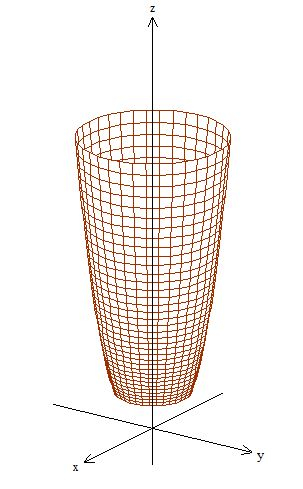
Sacou? :D

Passo 6

c )

Para saber se a superfície é regular ou não, precisamos encontrar o vetor normal N → ...

N → = ∂ r t ,   θ ∂ t × ∂ r t ,   θ ∂ θ

Como...

r t ,   θ = t cos ⁡ θ ,   t sin ⁡ θ ,   t 3

Então...

∂ r t ,   θ ∂ t = cos ⁡ θ ,   sin ⁡ θ ,   3 t 2

∂ r t ,   θ ∂ θ = - t sin ⁡ θ ,   t cos ⁡ θ ,   0

Como o produto vetorial é um determinante...

N → = i → j → k → cos ⁡ θ sin ⁡ θ 3 t 2 - t sin ⁡ θ   t cos ⁡ θ 0     ⇒

N → = i → j → k → cos ⁡ θ sin ⁡ θ 3 t 2 - t sin ⁡ θ   t cos ⁡ θ 0 i → j →   cos ⁡ θ sin ⁡ θ   - t sin ⁡ θ   t cos ⁡ θ  

Multiplicando cruzado lá...

N → = - 3 t 3 sin ⁡ θ j → + t cos 2 ⁡ θ k → - 3 t 3 cos ⁡ θ i → - t sin 2 ⁡ θ k →   ⇒

N → = - 3 t 3 cos ⁡ θ i → - 3 t 3 sin ⁡ θ j → + t cos 2 ⁡ θ k → + t sin 2 ⁡ θ k →   ⇒

N → = - 3 t 3 cos ⁡ θ i → - 3 t 3 sin ⁡ θ j → + t cos 2 ⁡ θ + sin 2 ⁡ θ k →   ⇒

N → = - 3 t 3 cos ⁡ θ i → - 3 t 3 sin ⁡ θ j → + t   k →  

Esse é o Vetor normal. Em uma notação mais simpática é...

N → = - 3 t 3 cos ⁡ θ ,   - 3 t 3 sin ⁡ �� ,   t

Com esse vetor em mãos, para saber se a parametrização é regular ou não, vejamos...

Passo 7

A supefície se diz regular quando o vetor normal não zera em nenhum ponto dessa superfície.

N → = - 3 t 3 cos ⁡ θ ,   - 3 t 3 sin ⁡ θ ,   t

Cara, a única forma de zerar esse vetor aí é se o t fosse 0 , mas como pelo próprio enunciado...

t ∈ 1 ,   2

Podemos afirmar que essa parametrização é regular ;)

Passo 8

d )

Bem, todo plano no espaço tem essa cara:

a x + b y + c z + d = 0

Para determinarmos o plano tangente pedido, o que precisamos fazer é determinar esse   a , b , c e d aí. Ou pelo menos eliminá-los da brincadeira.

Um plano tem outra característica muito importante: esse a , b e c ai são nada mais nada menos que coordenadas do vetor normal a esse plano... N → p = a ,   b ,   c .

Como o plano é tangente a normal a superfície S , N → , naquele ponto de tangência é a mesma normal do plano...

N → 2 ,   π = N → p

Como a equação da normal do plano já está calculada... N → = - 3 t 3 cos ⁡ θ ,   - 3 t 3 sin ⁡ θ ,   t . Basta substituir o ponto...

N → 2 ,   π = N → p       ⇒               - 3 2 3 cos ⁡ π ,   - 3 2 3 sin ⁡ π ,   2 = N → p             ⇒

  24 ,   0 ,   2 = N → p      

Como N → p = a ,   b ,   c …

a = 24 ,   b = 0       e         c = 2

Substituindo na equação do plano...

a x + b y + c z + d = 0     →

24 x + 2 z + d = 0

Agora nos falta determinar d ...

Passo 9

Para determinar o d , nós precisamos de outra informação. Bem, pensa comigo, o plano é tangente ao ponto r 2 ,   π . Isso significa que ele passa por esse ponto também, mas que ponto é esse? Vejamos...

r t ,   θ = t cos ⁡ θ ,   t sin ⁡ θ ,   t 3       →

r 2 ,   π = 2 cos ⁡ π ,   2 sin ⁡ π ,   2 3 →

r 2 ,   π = - 2 ,   0 ,   8

Então esse é o ponto. Já que ele pertence ao plano, podemos substituir na equação do plano...

24 x + 2 z + d = 0   →

24 - 2 + 2 8 + d = 0   →

- 48 + 16 + d = 0

d = 32

Então uma equação para o plano tangente é...

24 x + 2 z + 32 = 0

Sacou?

Passo 10

e )

∬ S   x 2   d S

Para calcular essa integral de superfície, lembremos que ela pode se transformar em uma integral dupla da forma...

∬ S   x 2   d S = ∬ r   x t ,   θ 2 ⋅ N → d t d θ

Como x t ,   θ é...

x = t cos ⁡ θ

∬ r   t cos ⁡ θ 2 ⋅ N → d t d θ

No lugar de r , podemos colocar os limites de t e θ ...

∫ 0 2 π ∫ 1 2 t cos ⁡ θ 2 ⋅ N → d t d θ   →

∫ 0 2 π ∫ 1 2 t 2 cos 2 ⁡ θ ⋅ N → d t d θ

Portanto agora só nos falta encontrar o módulo do vetor normal...

Passo 11

Como...

N → = - 3 t 3 cos ⁡ θ ,   - 3 t 3 sin ⁡ θ ,   t

Então...

N → = - 3 t 3 cos ⁡ θ 2 + - 3 t 3 sin ⁡ θ 2 + t 2     ⇒

N → = 9 t 6 cos 2 ⁡ θ + 9 t 6 sin 2 ⁡ θ + t 2     ⇒

N → = 9 t 6 cos 2 ⁡ θ + sin 2 ⁡ θ + t 2     ⇒

N → = 9 t 6 + t 2     ⇒

N → = t 2 9 t 4 + 1     ⇒

Como t é maior que 0 ...

N → = t 9 t 4 + 1

Então...

∫ 0 2 π ∫ 1 2 t 2 cos 2 ⁡ θ ⋅ N → d t d θ     →

∫ 0 2 π ∫ 1 2 t 3 9 t 4 + 1 ⋅ cos 2 ⁡ θ d t d θ

Bora integrar?

Passo 12

Calculando a integral com relação a t considerando θ constante...

∫ 0 2 π cos 2 ⁡ θ ∫ 1 2 t 3 9 t 4 + 1 d t d θ =

Como é uma integral iterada...

∫ 0 2 π cos 2 ⁡ θ d θ ⋅ ∫ 1 2 t 3 9 t 4 + 1 d t

Lembrando que

cos 2 ⁡ θ = 1 + cos ⁡ 2 θ 2

Calculamos a primeira integral...

∫ 0 2 π 1 2 + cos ⁡ 2 θ 2 d θ ⋅ ∫ 1 2 t 3 9 t 4 + 1 d t →

1 2 θ + sin ⁡ 2 θ 4 0 2 π ⋅ ∫ 1 2 t 3 9 t 4 + 1 d t   →

π ∫ 1 2 t 3 9 t 4 + 1 d t   →

Para resolver essa integral de dentro, façamos uma substituição simples...

9 t 4 + 1 = u     →           d u = 36 t 3 d t         o u             t 3 d t = d u 36

Trocando também os limites de integração...

t = 1         →             u = 9 t 4 + 1 = 10

t = 2         →             u = 9 t 4 + 1 = 145

π ∫ 1 2 t 3 9 t 4 + 1 d t = π ∫ 10 145 u d u 36

π 36 2 3 u 3 / 2 10 145 = π 54 u 3 / 2 10 145

π 54 145 3 / 2 - 10 3 / 2

Resposta

a )   z 2 3 = x 2 + y 2

b )

c )

Parametrização Regular.

d )   24 x + 2 z + 32 = 0

e )   π 54 145 3 / 2 - 10 3 / 2

Exercícios de Livros Relacionados

A base de uma cerca circular de raio 10 m é dada por x = 10 c o s t ,y = 10 s e n t . A altura da cerca na posição x , y é dada pela função h x , y = 4 + 0,01 ( x 2 - y 2 ) , portanto a altura varia 3
Use uma calculadora para avaliar a integral de linha correta até quatro casas decimais. ∫ C x y arctan ⁡ z d s, onde C tem equações paramétricas x = t 2, y = t 3, z = t, 0 ≤ t ≤ π 4
Calcule o valor da integral de linha, onde C é a curva dada. ∫ C x y e y z d y C :x = t , y = t 2 , z = t 3 , 0 ≤ t ≤ 1
Calcular as integrais curvilíneas. ∫ C ( x 2 + y 2 + z 2 )d s , onde C é a interseção das superfícies x 2 16 + y 2 9 + z 2 16 = 1ey = 2 .
Calcular as integrais curvilíneas. ∫ C ( x 2 + y 2 - z )d s , onde C é a parte da interseção das superfícies x 2 + y 2 + z 2 = 8 zez = 4