Seja a curva regular dada pela interseção das superfícies
a) Faça um esboço das superfícies e da curva regular .
b) Descreva uma parametrização regular de (
c) Calcule as equações implícitas da reta tangente à parametrização , onde a componente atinge seu máximo.
d) Calcule a integral de linha.
Passo 1
Letra a)
Vamos começar pela equação da superfície
Se estivéssemos no , teríamos uma circunferência, certo?? Mas como estamos no , o fato de não aparecer na nossa equação significa que para qualquer valor de , essa equação ainda é válida, ou seja, teremos infinitas circunferências ao longo de o que configura um cilindro
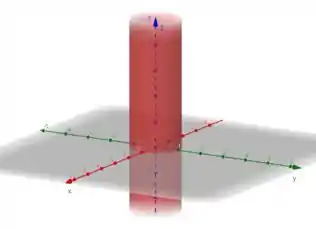
Indo agora para a nossa inequação
Se fosse uma equação , seria um plano paralelo a e que corta em . Como temos essa desigualdade , isso significa que é toda a região acima desse plano
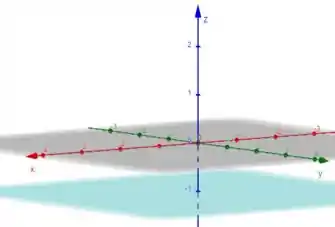
Para , o melhor é considerar como se estivéssemos no , isso seria uma reta no plano . Como se trata do e como não temos na equação, então teremos infinitas retas ao longo de o que caracteriza um plano
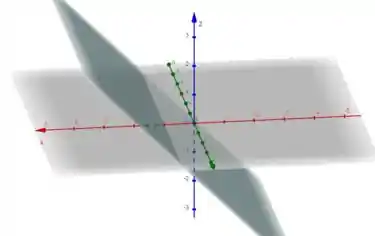
Juntando tudo temos
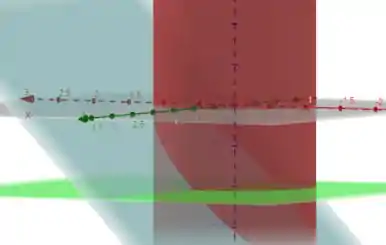

Passo 2
Passo 3
Letra b)
Utilizando coordenadas polares pensando só no cilindro projetado no plano
Agora que temos o plano cortando o cilindro, a parametrização dessa intersecção vai ser
O que eu fiz foi isolar e substituir
Como temos a equação como restrição, vamos substituir na coordenada da parametrização
Os valores de que satisfazem essa inequação são
A parametrização da curva então é:
Passo 4
Letra c)
Como a parametrização da curva é:
O valor de para o qual é máximo é , pois
Para encontrar uma reta tangente a esse ponto precisamos primeiro encontrar um vetor tangente, que é só calcularmos a derivada da parametrização de nesse ponto.
Para :
Agora a equação paramétrica da reta vai ser:
As equações implícitas são:
Passo 5
Letra d)
A integral que a questão está pedindo é uma integral de linha de uma função escalar ao longo da curva .
Podemos calcular ela dessa forma aqui:
Onde está parametrizada por:
E
Que é o módulo da derivada da parametrização da curva.
Resolvendo para o da questão:
Usando que
Substituindo na integral de linha:
Passo 6
Passo 7
Substituindo na equação da integral de linha, os valores para a parametrização da curva :
Manipulando um pouco a integral:
Usando uma substituição simples:
Resposta
Letra a)
Letra b)
Letra c)
Letra d)