Considere uma estrela situada à uma distância medida por um observador em repouso na Terra. Um astronauta parte da Terra em direção à estrela com velocidade .
Sob o ponto de vista do astronauta, qual é a distância percorrida e o tempo de viagem até a estrela?
Qual é a duração da viagem Terra-estrela medida pelo observador na Terra?
Se na metade da viagem (para o observador na Terra) o astronauta emitir um sinal de luz em direção à Terra, quanto tempo depois da partida do astronauta esse sinal será observado pelo observador na Terra?
Passo 1
Letra : Vamos entender primeiro o exercício. Inicialmente, temos um observador na Terra (referencial ) e o astronauta viajando no foguete com velocidade (referencial ). A estrela está uma distância , medida na Terra (no referencial ). Veja a figura abaixo.
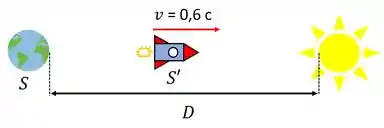
Agora, imagine por exemplo que o observador na Terra meça um certo comprimento . Para o astronauta na nave, ele medirá um comprimento , diferente de (na verdade, será menor que ). A relação entre e é dada por
Passo 2
Nesta parte, podemos simplesmente substituir (pois a distância foi medida em ) e usarmos que . Denotando por a distância entre a Terra e a estrela medida pelo astronauta, temos que
Já o tempo de viagem Terra-estrela medido pelo astronauta () é obtido pela distância entre a Terra e a estrela (medida pelo astronauta) dividida pela velocidade do astronauta , isto é,
Passo 3
Letra : Para o observador na Terra, o tempo de viagem Terra-estrela medido da Terra ) é dado pela distância entre a Terra e a estrela (medida da Terra) dividida pela velocidade do astronauta , isto é,
Passo 4
Letra Nesta parte, o tempo total que o sinal de luz demora para chegar na Terra depois da partida é igual ao tempo que o astronauta demora para chegar na metade do caminho entre a Terra e a estrela (que chamaremos de ) somado com o tempo que o sinal de luz demora para voltar até a Terra (que chamaremos de ), ambos medidos da Terra. Desta forma, temos que
Vamos obter primeiro . Note que, quando o sinal de luz é emitido, ele percorre metade da distância entre a Terra e a estrela, isto é, . Deste modo, o tempo que o sinal demora para chegar a Terra, medido da Terra, é
Vamos obter agora . Sabemos que o mesmo é a metade do tempo que o astronauta demora para realizar a viagem Terra-estrela, medido da Terra. Desta forma, utilizando o resultado do item , temos que
Desta forma, juntando todos os resultados, temos que
Resposta
- e