Uma esfera oca de ferro () é mantida submersa em um lago de água doce () amarrada a uma corda presa no fundo do lago. O raio externo da esfera é igual a . A tensão na corda é igual a . Considere .
Desenhe o diagrama de forças que atuam sobre a esfera.
Calcule a força de empuxo exercida pela água sobre a esfera.
Qual é a massa da esfera?
A corda se rompe e a esfera sobe até a superfície. Quando ela atinge o equilíbrio, qual é a fração do volume que fica submersa?
Calcule a espessura da casca esférica.
Passo 1
Para desenhar o diagrama de forças que atuam na esfera, vamos primeiro determinar que forças são essas!
As forças que atuam na esfera são:
- Força peso
- Empuxo
- Tração da corda
O diagrama de forças vai ficar assim:
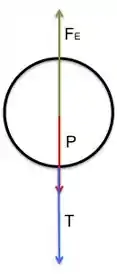
Passo 2
Pela definição de empuxo, lembramos que ele é igual, em módulo, ao peso do volume de líquido deslocado, ficou confuso?! Se liga que a fórmula, é a seguinte:
Para o caso da esfera, temos que o volume imerso é dado por:
O empuxo fica:
Passo 3
Para determinar a massa da esfera, devemos calcular através do equilíbrio. Sabemos que por estar em equilíbrio, temos a seguinte relação:
Obs: Você deve estar pensando que é mais fácil achar a massa da esfera multiplicando a densidade pelo volume...mas...não é bem assim. Por se tratar de um esfera oca, não sabemos o volume de ferro presente na casca esférica, por isso tivemos que calcular a massa através da relação de equilíbrio.
Passo 4
Na nova situação de equilíbrio, não teremos mais a tração atuando, a relação de equilíbrio vai ser então:
Onde é a nova força de empuxo.
O novo volume imerso vai ser:
A fração do volume total que está submersa vai ser então:
Passo 5
Como sabemos a massa de ferro presente na esfera, assim como a densidade do ferro e o raio externo da esfera, podemos determinar a espessura da casca esférica. Se liga!
Pela definição de densidade, temos:
Onde é o volume de ferro da casca esférica, seu valor é:
Agora que temos o volume, podemos calcular o raio interno , tendo em vista que o raio externo foi dado!
Substituindo os valores, temos:
A espessura da casca é dada por:
Resposta
Ver figura acima