Um solenóide toroidal tem seção transversal quadrada de lado , raio interno , raio externo e voltas de um fio condutor fino enroladas de forma compacta em torno dele. Por cada uma das espiras passa uma corrente , que produz um campo magnético no interior desse toróide. Nessa situação e sabendo que esse campo magnético não é uniforme ao longo da seção reta de cada espira, qual é a energia magnética acumulada na região interna desse toróide?
Passo 1
Vamos tentar entender a situação do problema olhando para a figura abaixo. Representamos apenas uma seção transversal de um toróide, neste caso apenas metade do toróide e apenas algumas das espiras quadradas. Cada uma das espiras quadradas transporta uma corrente e as colocamos no sentido horário indicado na figura.
Por isso, pela regra da mão direita, o campo magnético que essas correntes geram está entrando no plano da página. Para facilitar nossa discussão, colocamos também a área sempre paralela ao campo magnético , como ilustrado na figura. Colocamos também uma área infinitesimal pela qual o campo passará.
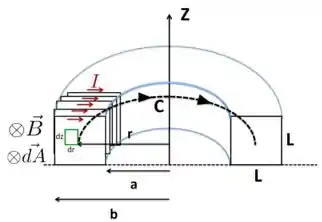
A corrente em cada uma das espiras atravessará uma área definida pelo contorno fechado , que está a uma distância do eixo .
Passo 2
Bom, agora que já visualizamos a questão através da figura (assim espero...rsrs), vamos entender o que precisamos calcular neste caso.
Primeiro, para obter a autoindutância , vamos começar nossa solução pela expressão do fluxo magnético e sua relação com a autoindutância de acordo com
sendo que é corrente que percorre cada uma das espiras quadradas do solenóide toroidal.
O caminho que a gente vai seguir abaixo é o seguinte: calculamos o fluxo total do toróide e o igualamos a para tirar a expressão para .
Então, obtemos o seguinte módulo para o campo magnético
Tendo o valor do campo gerado pela corrente que passa nas espiras, podemos encontrar o fluxo magnético. Como o elemento de área é sempre paralelo a e este tem mesmo valor em todos os pontos da curva neste caso, temos que
Como o módulo do campo magnético não é uniforme dentro do toróide, pois depende da distância como acabamos de ver, então não podemos tirar o de dentro da integral, blz?? Fica ligado nessa informação... Sei que a gente fica tentado em tirar o da integral porque facilita e muito nossa vida, mas não faça isso a menos que o enunciado te diga que é uniforme...IMPORTANTÍSSIMO ISSO...
Dá uma olhada lá na figura e veja que, neste sistema de coordenadas, o elemento infinitesimal de área atravessada pelo campo é . Por isso, o fluxo total é
Resolvendo a integral acima, obtemos que o fluxo magnético total através das espiras é
que nos permite encontrar a expressão para a autoindutância.
Passo 3
Como a energia magnética acumulada no campo magnético é dada por
temos, utilizando a expressão da indutância encontrada no passo anterior, que