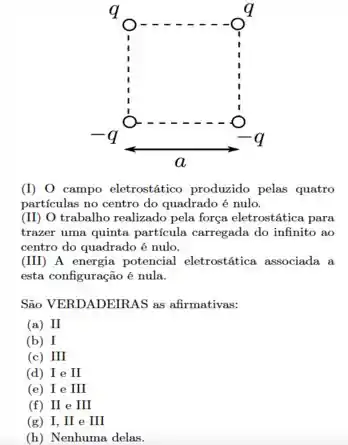
Quatro partículas carregadas são fixadas sobre os vértices de um quadrado de lado , como mostrado na figura abaixo. Suas cargas estão indicadas. Considere que a energia potencial eletrostática é nula quando as partículas estão infinitamente afastadas entre si. Sobre essa situação, considere as afirmativas abaixo:
Passo 1
Bom, vamos começar a estudar essa questão considerando a figura abaixo, em que identificamos as cargas de mesmo sinal com a mesma cor e também enumeramos cada uma delas. Vamos dizer que , para facilitar a nossa discussão, mas o mesmo valerá para o caso em que .
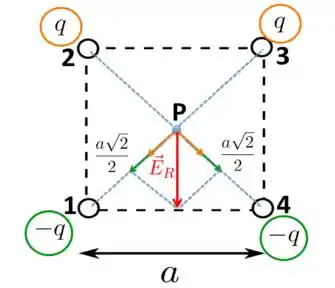
Na figura acima, representamos o centro do quadrado por um ponto . Este ponto está a uma mesma distância de cada uma das cargas. Como , os campos gerados pelas cargas 2 e 3 (ambas positivas) em laranja sobre o ponto são de afastamento, como indicam os vetores de mesma cor.
Já as outras cargas 1 e 4, as de sinal (portanto negativas), produzem campos de aproximação (vetores em verde), também representados na figura.
Fica claro da figura que, ao somarmos os vetores, no ponto teremos um campo resultante . Portanto, no centro do quadrado, existe um campo elétrico diferente de zero!!
Repare que a gente nem precisou fazer conta para saber se há campo resultante e nem precisaríamos, pois o item () apenas afirma algo (ERRADO, no caso), sobre a existência de campo no ponto .
Passo 2
Agora vamos olhar para o item (). Então, precisamos saber como é o trabalho realizado sobre a quinta partícula nesse caso. Como haverá uma força eletrostática atuando sobre a quinta carga , estamos falando de uma força conservativa, a qual realizará um trabalho dado pela seguinte expressão
que é o trabalho realizado pela força eletrostática para levar do infinito para o ponto , e é o potencial produzido pelas cargas 1, 2, 3 e 4 em cada uma das posições de .
Como o potencial , ou seja, o potencial que as partículas 1, 2, 3 e 4 geram no infinito é zero, precisamos apenas saber como é o potencial que elas geram no ponto , que é o centro do quadrado e é para onde será levada.
Bom, a gente já viu que no centro do quadrado, o campo elétrico é diferente de zero! (Dá uma olhada na figura!) Agora, como fica o potencial ? Diferente do campo elétrico, o potencial elétrico é uma grandeza escalar, de maneira que a análise vetorial que fizemos na figura não se aplica para . Na verdade, é até mais fácil analisar esse caso para o potencial. Quer ver?
Olha na figura e veja que temos quatro cargas, todas com mesmo módulo, mas um par com carga de sinal de oposto ao outro par. Como elas estão à mesma distância () de , temos o seguinte
Como , temos que o trabalho é
o que torna o item () correto.
Passo 3
O item ( afirma algo sobre a energia potencial eletrostática da configuração formada pelas cargas 1, 2, 3 e 4. A energia eletrostática de interação entre duas cargas e quaisquer distantes uma da outra por um tamanho é dada por
Precisamos, então, aplicar essa expressão para as cargas do quadrado. Mas CUIDADO: a energia eletrostática total será a soma das energias de cada par contadas uma única vez. Isso significa que: a gente só vai contar a energia de um ÚNICO par de cargas uma ÚNICA VEZ! OK? Vou montar um esquema para você :-)
Olha para figura abaixo e tenta seguir a identificação das cargas e suas interações à direita!
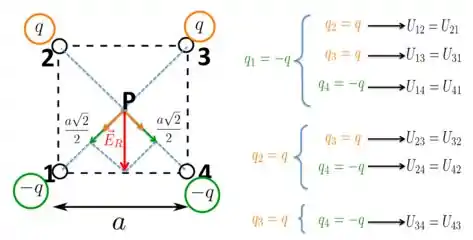
Para você entender como funciona o esquema da figura à direita acima: você fixa uma carga, por exemplo , da configuração, e faz o cálculo da energia de interação dessa carga com a carga e obtém a energia . Acompanhou?
Agora, essa energia é a mesma que aquela quando você fixa a carga e faz o cálculo da energia dela com a carga , já que temos o seguinte:
Ou seja, só contamos a interação de 1 com 2, já que é a mesma que a de 2 com 1.
Portanto, repetindo esse esquema para todas as cargas, obtemos a energia eletrostática total do sistema, que é:
Utilizando a expressão para a energia potencial para cada um dos termos da equação acima (tomando cuidado com as distâncias entre as cargas!!), obtemos que
Portanto, mostramos que a energia eletrostática associada a esta configuração é diferente de zero, que nega a afirmação dada no item () desta questão.
SUGESTÃO: Para uma distribuição discreta qualquer de cargas estáticas, procure seguir esse procedimento para o cálculo da energia eletrostática do sistema. Isso pode te ajudar a contabilizar todas as contribuições. Você vai ver que não tem erro fazendo assim...
Resposta
Portanto, a resposta correta é a letra a) .