02) Uma barra delgada AB de comprimento gira em torno do eixo vertical com velocidade angular constante . Em sua extremidade B está articulado um disco de raio que gira em torno do eixo perpendicular ao plano da figura com velocidade angular constante . Adotando a base solidária à barra AB, determinar, para a configuração indicada:

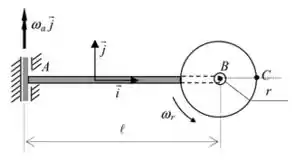
a) O vetor rotação absoluta do disco;

b) O vetor aceleração rotacional absoluta do disco;

c) A velocidade absoluta do ponto C;

d) A aceleração absoluta do ponto C.

b) Aqui devemos calcular o vetor aceleração rotacional absoluta do disco. E, novamente, como o disco executa dois movimentos de rotação diferentes, teremos que:

Como e são constantes, temos . Daí:

Show! Bora pro próximo item.

c) Precisamos determinar a velocidade absoluta do ponto C.

Usando a expressão do movimento plano geral, podemos escrever que:

Mas, ainda não sabemos quem é . Porém, como A é um ponto fixo, podemos escrever que:

Substituindo em , vem que:

Logo:

Excelente! Agora só falta o último item. Bora lá pessoal, gás final!

d) Devemos calcular a aceleração absoluta do ponto C.

A ideia é a mesma do item anterior: usar a expressão do movimento plano geral. Daí:

Mas, não sabemos quanto vale . Porém, como o ponto A é fixo, podemos escrever que:

Substituindo em , ficamos com:

Aí sim gente! Terminamos mais uma questãozinha, até que não deu tanta conta né?!Até a próxima pessoal!