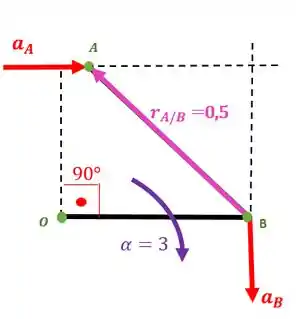
Determine a aceleração angular da barra e a aceleração linear de para se e nessa posição. Desenvolva sua solução usando notação vetorial.
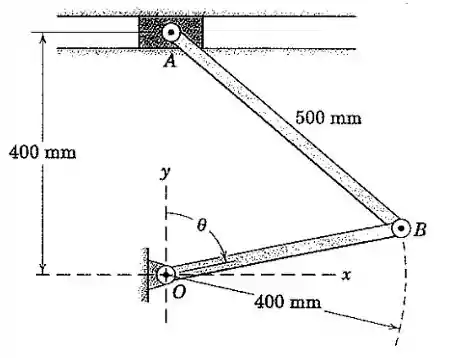
Passo 1
Vamos começar analisando as velocidades. Repare que as barras não possuem velocidade angular, pois foi dito no enunciado que :
Vamos ter que a velocidade do ponto será:
Como a velocidade angular é nula, vamos ter que:
Como o ponto realiza um movimento circular em torno do ponto , podemos calcular a velocidade deste ponto assim:
Opa, mas a velocidade angular da barra é zero. Então:
Passo 2
Agora vamos fazer a análise das acelerações. Quando vamos ter:
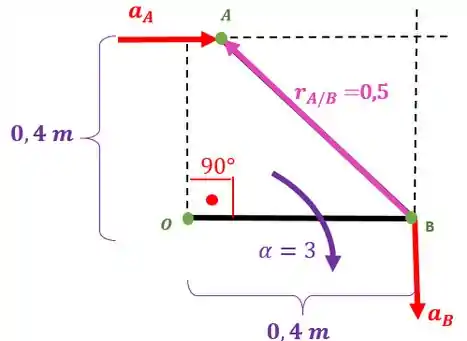
Podemos achar a aceleração do ponto , já que sabemos a aceleração angular da barra
Vetorialmente temos que o vetor aponta no sentido negativo do eixo :
Nossa equação da aceleração do ponto vai ser:
Como , então nos resta:
Passo 3
Vamos decompor nossos vetores no eixo para fazer a soma vetorial. Vamos começar pelo vetor :
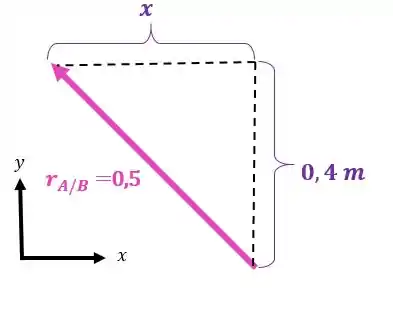
Por teorema de Pitágoras conseguimos achar o valor de :
Então, podemos escrever nosso vetor assim:
Sabemos que o vetor aceleração angular da barra está no eixo . Vamos arbitrar um sentido para ele e depois verificamos se está certo. Vamos colocar o vetor como positivo no eixo :
E o vetor aceleração do ponto (Esse é o vetor que queremos determinar, mas sabemos que ele está no eixo , pois o ponto só pode se mover na horizontal:
Então, vamos ter que:
Passo 4
Vamos fazer o produto vetorial:
Nossa matriz vai ficar:
Vamos substituir isso na nossa equação:
Agora é só separarmos as equações de acordo com suas componentes:
Da segunda equação podemos determinar o valor de :
O sinal negativo indica que escolhemos o sentido errado do vetor , ou seja, ele aponta no sentido negativo do eixo :
Pela primeira equação vamos achar o valor da aceleração no ponto :
Repare que o valor deu positivo, isso significa que o sentido que arbitramos para o vetor está certo. Ou seja, ele deve ficar assim: