Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Quádricas

Ver Teoria
Exercício 1412345678910111213151617181920

Enunciado

Considere a quádrica

Ω : x 2 9 - y 2 9 + z 2 16 = 0

a) Identifique e esboce Ω .

b) Determine os traços (cortes com planos paralelos a algum plano coordenado) de Ω que são cônicas com distância focal 10.

Passo 1

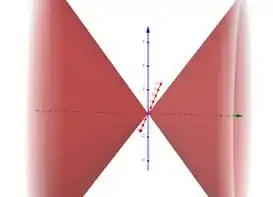
a) Ω é um cone elíptico ao longo do eixo y .

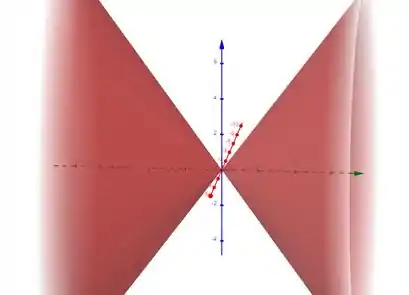
Passo 2

b) Fazendo x = k temos

k 2 9 = y 2 9 - z 2 16

y 2 k 2 - z 2 16 k 2 9 = 1

Isso é a equação de uma hipérbole onde os parâmetros são a 2 = k ² , b 2 = 16 k 2 9 e c 2 = a 2 + b 2 = 25 k 2 9 → c = 5 | k | 3 . Para que essa hipérbole tenha distância focal 10, 2 c deve valer 10, ou seja:

2 . 5 | k | 3 = 10

k = 3

Logo, os traços aqui são x = 3 e x = - 3 (planos em azul na imagem abaixo, a sua intersecção com o cone forma uma hipérbole com distância focal 10).

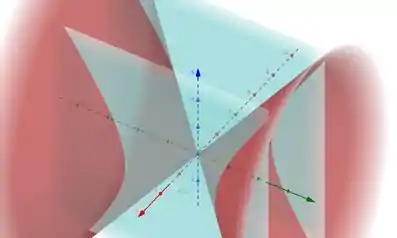
Passo 3

Fazendo y = k temos

x 2 9 + z 2 16 = k 2 9

x 2 k 2 + z 2 16 k 2 9 = 1

Isso nos dá a equação de uma elipse com parâmetros a 2 = 16 k 2 9 , b 2 = k ² e c 2 = a 2 + b 2 = 7 k 2 9 → c = 7 k 3 .

Para que a distância focal seja 10, 2 c = 10 :

2 . 7 k 3 = 10

k = 15 7

Ou seja, y = 15 7 ou y = - 15 7 (planos em azul na imagem abaixo, a sua intersecção com o cone forma uma elipse com distância focal 10).

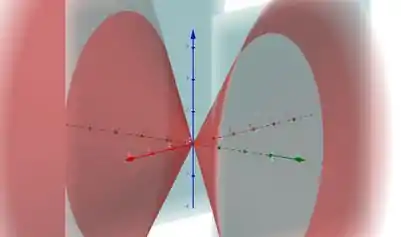
Passo 4

Fazendo z = k temos

k 2 16 = - x 2 9 + y 2 9

- x 2 9 k 2 16 + y 2 9 k 2 16 = 1

Temos aqui equações de hipérboles com a 2 = 9 k 2 16 , b 2 = 9 k 2 16 e c 2 = 18 k 2 16 → c = 3 2 k 4 .

Para que a distância focal seja 10:

2 . 3 2 k 4 = 10

k = 10 2 3

Ou seja, em z = 10 2 3 e z = - 10 2 3 (planos em azul na imagem abaixo, a sua intersecção com o cone forma uma hipérbole com distância focal 10).

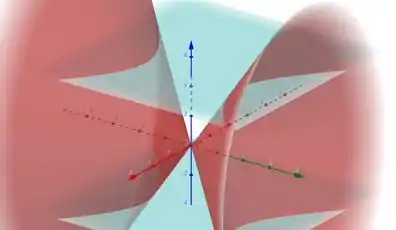
Resposta

a) Cone Elíptico.

b) x = 3 e x = - 3

y = 15 7 e y = - 15 7

z = 10 2 3 e z = - 10 2 3

Exercícios de Livros Relacionados

Escolhendo convenientemente os eixos, mostre que a interseção de um plano com uma quádrica central é uma cônica. Em particular, mostre que a interseção de um plano com um elipsoide é uma elipse.
Escreva as equações de mudança de eixos (rotações) que eliminam os termos em x y ,x zey z nas formas quadráticas do Exercício 44.1.
Para cada uma das equações abaixo, efetue uma rotação de eixos de modo a eliminar os termos em x y ,x z ,y z . Em seguida, efetue translações de modo a eliminar, ou reduzir a um só, os termos em x, y
Para cada uma das equações abaixo, efetue uma rotação de eixos de modo a eliminar os termos em x y ,x z ,y z . Em seguida, efetue translações de modo a eliminar, ou reduzir a um só, os termos em x, y
Para cada uma das equações abaixo, efetue uma rotação de eixos de modo a eliminar os termos em x y ,x z ,y z . Em seguida, efetue translações de modo a eliminar, ou reduzir a um só, os termos em x, y