Ache real tal que as superfícies esféricas e sejam tangentes:
Passo 1
Devemos determinar o valor de para que as superfícies dadas sejam tangentes vamos usar o que aprendemos na teoria. Bora colocar a teoria em prática!! ;)
Passo 2
Da teoria, sabemos que duas superfícies são tangentes, se considerando e :
![]()
Da teoria também conseguimos calcular a distância por meio da fórmula:
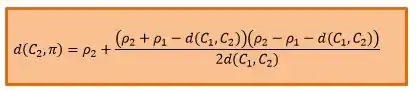
Então, para calcular essa distância precisamos de: . Vamos, então, encontrar esses valores.
Para , temos:
Para teremos que completar quadrado:
Já vamos aproveitar e calcular :
Passo 3
Agora, que temos todos os valores que precisamos podemos calcular a distância :
Susbtituindo na fórmula os valores:
Como queremos que os planos sejam tangentes temos ainda que :
Resolvendo:
Separando em dois casos:
Resolvendo
Resolvendo
Chegamos que para as superfícies e sejam tangentes devemos ter que: