Obtenha equações gerais dos planos tangentes à superfície esférica
Que são paralelos ao plano .
Passo 1
O enunciado pede para obtermos as equações gerais dos planos que são:
- Tangentes à superfície esférica
- Paralelos ao plano .
Passo 2
Vamos começar olhando para a segunda informação que nos foi dada!! Como vimos na teoria sobre planos, se dois planos são paralelos significa que seus vetores normais também são paralelos e como foi dada a expressão geral do plano e essa expressão é do formato:
Sendo as coordenadas do vetor normal, então, a equação dos nossos planos que queremos encontrar será:
Passo 3
Falta, agora, determinarmos o valor de . Para isso, vamos usar a informação em relação à superfície esférica. Sabemos que é tangente aos planos que queremos encontrar e da teoria sabemos que para que um plano e uma esfera sejam tangentes devemos ter:
Então, temos que achar as coordenadas do centro e valor do raio para calcularmos a distância d ponto até o plano que queremos determinar. Para achar e vamos completar quadrados:
Portanto,
Passo 4
Sabendo que e que , vamos usar aquela fórmula, lembra, para calcular distância entre ponto e plano, essa aqui oh:
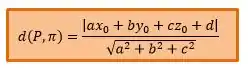
Substituindo os valores, temos:
Como são tangentes:
Então,
Chegamos então nas duas possibilidades de planos tangentes à e paralelos ao plano :