Dê uma equação da superfície esférica tangente aos planos
Cujo centro pertence à reta
Passo 1
Esse exercício é um pouco diferente do que vínhamos fazendo. Queremos novamente determinar a equação da superfície esférica. Mas, agora, as informações que nos são dadas para isso são:
- Superfície tangente aos planos
- Centro da superfície pertence à reta
Teremos que usar essas informações para achar as coordenadas do centro e o raio da esfera. Mas, como faremos isso?

Relaxa!! Vamos fazer o passo a passo!! ;)
Passo 2
Para resolver esse tipo de problema sempre bom fazer um esboço das informações que temos para tentar abstrair e ver como podemos chegar a uma solução!! Então, a figura a seguir seria um bom esboço!
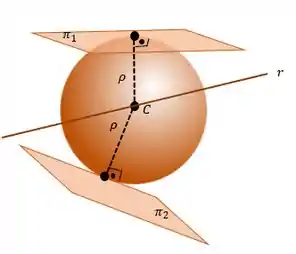
Vamos começar determinando o centro . Sabemos que pertence à reta . Com a relação que nos foi dada, chegamos que:
Então, um ponto genérico da reta possui as seguintes coordenadas:
Então,
Passo 3
Agora, vamos utilizar os planos. Sabemos que os planos são tangentes à esfera. Então, isso significa que a distância entre o plano e é igual a distância entre e , portanto:
Como temos a distância entre um ponto e um plano usaremos a seguinte fórmula:
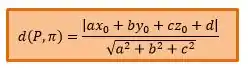
Para o plano :
Para o plano :
Substituindo os valores acima na fórmula e considerando :
Elevando os dois membros ao quadrado e resolvendo:
Temos duas possibilidade para :
Passo 4
Para determinar uma superfície esférica precisamos de e do raio, então vamos calcular uma das distâncias ou , escolhendo e calculando temos:
Para
Para
Portanto, temos como solução duas superfícies esféricas possíveis: