Três objetos em “T” são feitos, cada um, com duas hastes idênticas, de mesma massa e mesmo comprimento. Eles giram com velocidade angular constante em torno dos eixos tracejados. Sabendo que todas as configurações têm a mesma energia cinética de rotação, o que se pode dizer sobre o módulo da velocidade angular em cada caso?
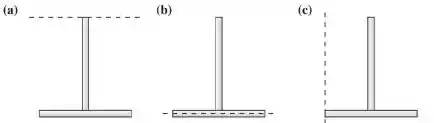
(A)
(B)
(C)
(D)
(E)
Passo 1
Energia cinética de rotação é dada por:
O enunciado diz que todos os três objetos têm a mesma energia cinética de rotação , então:
Queremos saber qual das velocidades angulares é maior ou menor para que todos eles tenham a mesma energia cinética .
Então, precisamos descobrir os momentos de inércia com relação a cada um dos eixos em (a), (b) e (c) para relacionar as velocidades angulares .
Aqui, podemos fazer analisando qualitativamente ou então fazendo as contas.
O jeitinho analisando é mais rápido, mas vamos fazer os dois pra ficar fera nisso.
Passo 2
O momento de inércia nos três casos será a soma dos momentos de cada haste.
Nos três casos, temos uma das hastes com o eixo passando por sua extremidade, portanto elas terão o mesmo momento de inércia :
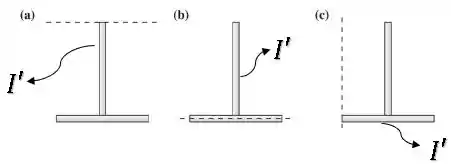
Então, contabilizando apenas essas hastes, os momentos de inércia nos três casos estão iguais.
As hastes restantes que farão a diferença.
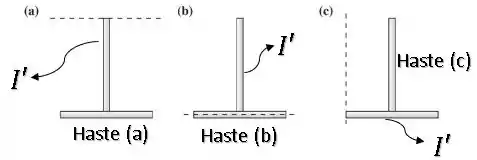
Dentre as hastes restantes, a que está mais afastada do eixo de rotação terá o maior momento de inércia, então:
Agora, vamos voltar à expressão das energias cinéticas:
Quanto maior o momento de inércia , menor tem que ser a velocidade angular para manter o mesmo valor de energia cinética .
Então, temos que a relação inversa dos momentos de inércia:
Achamos a letra (E) como resposta.
Passo 3
Para quem quiser fazer umas continhas de momento de inércia, esse é um bom treino...
Antes de calcular esses momentos de inércia, vamos calcular um caso que aparece nos três casos...
O momento de inércia de uma haste com relação a um eixo perpendicular passando pelo seu centro de massa é:
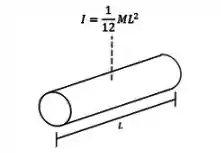
Para o momento de inércia de uma haste com o eixo perpendicular passando pela extremidade, precisamos usar o teorema dos eixos paralelos:
Passo 4
O momento de inércia no caso (a), será a soma dos momentos de inércia das duas hastes do “T” com relação ao eixo horizontal passando pelo topo do objeto:
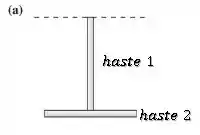
O momento de inércia da haste 1 é exatamente o caso que calculamos no Passo 2:
O momento de inércia da haste 2 é dado por:
Eita! Integral?
Não se assusta, calma.
Isso é uma forma de multiplicar cada elementozinho de massa da barra pela sua distância do eixo ao quadrado.
Mas como todos os elementos da haste 2 estão a uma mesma distância do eixo, igual ao comprimento da haste 1:
Podemos tirar essa constante da integral:
E integral de é o somatório de todos os elementozinhos de massa da haste, ou seja sua própria massa:
OBS: Como todos os pontos da haste estão a uma mesma distância do eixo, ela terá o mesmo momento de inércia que uma partícula de massa a uma distância do eixo.
Então, o momento de inércia total desse objeto será:
Passo 5
O momento de inércia no caso (b), será a soma dos momentos de inércia das duas hastes do “T” com relação ao eixo horizontal passando pela haste inferior:
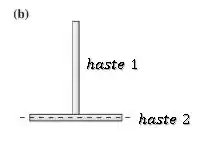
O momento de inércia da haste 1 é exatamente igual ao caso que calculamos no Passo 2:
Já o momento de inércia da haste 2 será um pouco diferente. Como a largura/diâmetro dessa haste é desprezível, é como se todos os elementos de massa da haste estivessem posicionados sobre o eixo de rotação.
Assim, o momento de inércia da haste 2 com relação ao eixo passando por ela é nulo:
Então, o momento de inércia total no caso (b) é:
Passo 6
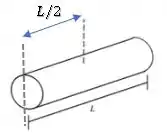
O momento de inércia no caso (c), será a soma dos momentos de inércia das duas hastes do “T” com relação ao eixo vertical passando pela extremidade da haste inferior:
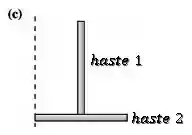
O momento de inércia da haste 1 é dado por:
Assim como já fizemos anteriormente, a distância da barra ao eixo é constante, então podemos tirar da integral:
Como a distância da haste 1 ao eixo é metade do comprimento da haste 2, temos:
Enquanto isso, o momento de inércia da haste 2 será aquele mesmo caso que já calculamos no Passo 2:
Logo, o momento de inércia total no caso (c), será:
Passo 7
Agora que temos o momento de inércia de cada caso, podemos comparar as velocidades angulares:
Para manter a igualdade, o objeto que tiver maior momento de inércia terá que ter a menor velocidade angular , mas vamos fazer essas continhas de qualquer forma para achar exatamente quanto.
Vamos comparar tanto quanto com :
Então, temos que é maior que :
Enquanto isso:
Então, é maior que , porém, menor que :
Ou então:
Ficamos com a letra (E).
Resposta
Letra (E)