Determine a coordenada do centro de massa da casca esférica, que tem espessura uniforme, mas fina.
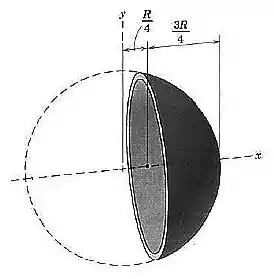
Passo 1
Podemos representar a esfera por uma imagem bidimensional da mesma:
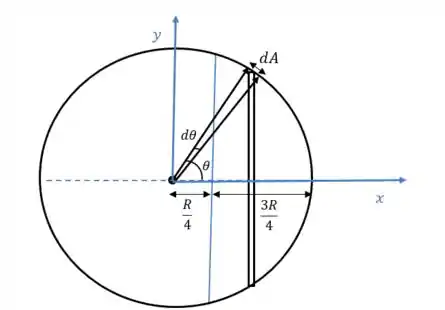
Perceba que, para uma pequena variação , existe uma pequena área superficial relacionada.
Agora vamos começar a pensar em termos de massa: uma quantidade infinitesimal de massa será dada por:
Perceba que é a espessura da “fatia” infinitesimal da esfera e que é a circunferência.
Opa, mas veja só isso: de acordo com o nosso desenho, podemos escrever: , né?
Então:
Show de bola, agora já sabemos que temos que integrar isso daí pra conseguirmos a massa.
Passo 2
Beleza, vamos integra isso em
Mas qual é o intervalo de integração? Bom, o ângulo varia desde zero até o ângulo final que gera aquele espacinho de
Esse ângulo final pode ser calculado pela tangente do triângulo final formado:
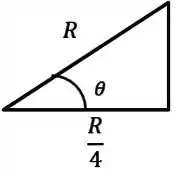
Quanto vale o cosseno desse ângulo?
Assim:
Show?
Agora já podemos aplicar:
Passo 3
Analogamente ao que fizemos com , podemos escrever na forma:
Então:
Lembrando que:
Podemos escrever:
Integrando:
Passo 4
Aplicando a nossa equação de :