1) No sistema em equilíbrio mostrado na figura, a placa homogênea , de massa , está no plano e tem seu movimento restrito pela articulação em , pelo anel em e pela barra . A barra é paralela ao eixo e tem peso desprezível. Sobre a placa atuam a força , o peso e o binário . Determinar:
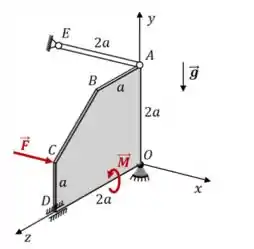
a) As coordenadas do centro de massa da placa no sistema .
b) O diagrama de corpo livre da placa.
c) As equações de equilíbrio da placa.
d) Os esforços atuantes na barra .
e) As reações vinculares em e .
Passo 1
Faaaala galerinha do Responde Aí. Como é que vocês estão? Bora dar o gás em mecânica!!
a) Nesse item a questão pede para encontrarmos as coordenadas do centro de massa da placa. Para fazer isso, precisamos determinar separadamente os valores de e .
Como a placa está apenas no plano , podemos logo de cara dizer que:
Massa, foi rapidinho! Os próximos dois valores (e vão exigir que a gente tenha uma sacadinha importante. Lembra que, por definição, o centro de massa de um corpo obedece à equação:
Ou seja, podemos dividir a nossa placa em pedaços que sejam mais convenientes, e calcular o centro de massa usando essa equação. Esses “pedaços” convenientes geralmente são triângulos e quadrados, porque sabemos da geometria que os centros de massa nesse caso coincidem com o centro geométrico, que já são conhecidos.
Então, bora fazer isso, mas vamos buscar calcular o C.M do quadradão total de lado que envolve a placa. Essa é a sacada que precisamos ter!
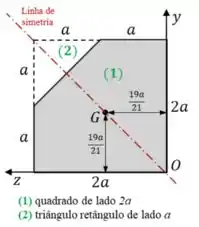
Montando a equação do centro de massa para esse quadrado grande, e fazendo isso inicialmente para o valor da coordenada em , temos:
Manipulando um pouquinho, ficamos com:
Excelente! Conseguimos reduzir bastante nosso trabalho, porque pensa comigo:
A área 1 é um quadrado, então o seu centro de massa tá bem no meio. Logo:
Já a área 2 é um triângulo, então o seu centro de massa fica no baricentro. Daí, pela semelhança temos a seguinte configuração:
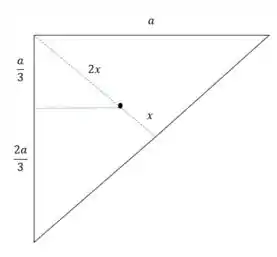
Então, lembrando que no vértice oposto a hipotenusa do nosso triângulo temos , vem que:
Para podermos usar nossa querida equação do C.M, só falta acharmos quanto vale . Podemos fazer também descontando a área do triângulo da área do quadrado de lado . Ou seja,
Olha que top. Como já temos podemos substituir na equação abaixo:
Daí vem que:
Aeee, finalmente achamos:
Agora vem a notícia boa, não vamos ter trabalho algum pra calcular , pois devido à simetria podemos afirmar diretamente que:
Ufaa! Por fim, achamos então que as coordenadas do centro de massa da nossa plaquinha valem:
Passo 2
Bora aproveitar o gás e detonar essa letra B.
b)
Aqui precisamos desenhar o diagrama de corpo livre (DCL) da nossa plaquinha. Mas o DCL é simplesmente um esquema mostrando as forças e momentos que estão atuando em nosso corpo rígido. Esses esforços podem ser de dois tipos:
1) Esforços devido às reações de apoio
2) Esforços externos aplicados no nosso corpo
Vamos começar pensando no grupo 1.
Em D temos um apoio do 2° gênero, ele só consegue impedir o movimento da placa nos eixos e .
Em O, o apoio é do 3° gênero, logo ele consegue impedir o movimento da placa nos três eixos.
Em A, a placa está articulada numa barra, assim só vamos ter uma força tipo de Tração mesmo, da barra puxando nossa plaquinha.
Para cada uma dessas forças, vamos supor que apontem no sentido positivo dos seus respectivos eixos.
Top!
Já o grupo 2 são os esforços externos, que estão indicados no enunciado.
Então, agora é só desenharmos a plaquinha indicando tudo isso:
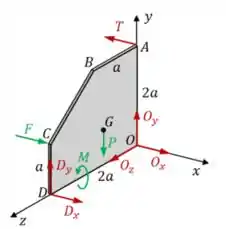
Prontinho 😊
Passo 3
c)
Precisamos determinar as equações de equilíbrio da placa. Essas equações de equilíbrio, basicamente devem mostrar que as resultantes dos esforços atuantes na placa são nulas. Então, começando pela força temos:
Nosso trabalho vai ser escrever como seria a resultante das forças em cada um dos eixos. Mas não é tão complicado quanto parece galera, é só a gente olhar o DCL e somar todas as forças que apontam para o mesmo sentido de um dos eixos, e subtrair as que apontam para o sentido oposto desse mesmo eixo. Se liga só:
Massa demais! Só tem que ter cuidado pra não esquecer de nenhuma forcinha ou trocar algum sinal. Porque depois disso vamos fazer um monte de conta, e se tiver uma só equação errada, os resultados vão dar todos alterados ☹
Beleza, mas vamos agora considerar a resultante dos momentos nula. Daí:
Novamente, escrevendo a equação para cada um desses eixos e lembrando que o momento de uma força é dado pelo produto (onde é o vetor braço da força) no qual usamos a regra da mão direita pra determinar o seu sentido, temos:
Pronto!! Agora já temos todas as nossas equações de equilíbrio:
Já foi mais uma! 😊
Passo 4
d)
Aqui precisamos determinar os esforços atuantes na barra . Mas, basicamente temos apenas a tração , puxando a barra através da articulação do nó em A. E para que haja o equilíbrio da barra, em o apoio também deve puxar a barra (no sentido .
Será que vamos precisar resolver todo o sistema pra encontrar o valor de
Nãoo, ainda bem haha.
Como e são dados da questão, olhando a equação (5), conseguimos isolar (UFAA).
Daí, vem:
Passo 5
e)
Nesse item precisamos determinar as reações nos apoios e . Infelizmente (falo pela preguiça que existe em mim e em você), vamos ter que resolver esse sistema linear encontrado no item C. Mas bora lá, sem deixar a peteca cair!!
Da equação (3), vem que:
Substituindo esse resultado na equação (2), vem que:
Da equação (4), temos também que:
Substituindo os resultados encontrados até aqui em (1), vamos ficar com:
Ufa, até que não deu tanto trabalho, já conseguimos determinar quanto valem essas reações. Lembrando que, se encontrarmos um valor positivo é porque o sentido que supomos inicialmente está correto, se encontrarmos um valor negativo, é porque o sentido que encontramos inicialmente está invertido.
Portanto, finalmente temos:
É isso!! Terminamos mais uma questão, espero que vocês tenham entendido tudo bem direitinho.Até a próxima galera 😉
Resposta
a)
b) Resolução no Texto.
c) Resolução no Texto.
d)
e)