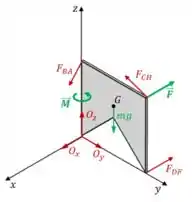
01) No sistema em equilíbrio mostrado na figura, a placa homogênea , de massa , está no plano e tem seu movimento restrito pela articulação em e pelas barras articuladas e . Todas as barras possuem peso desprezível e a barra é paralela ao eixo . Sobre a placa atuam a força o peso e o momento binário . Determinar:
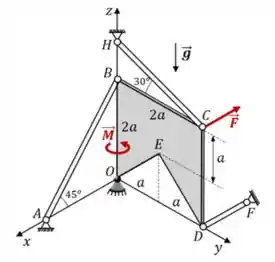
a) As coordenadas do centro de massa da placa no sistema .
b) O diagrama de corpo livre das barras e da placa.
c) As equações de equilíbrio da placa.
d) Os esforços atuantes nas barras.
e) As reações vinculares em .
Passo 1
Faaala galera, tudo certinho com vocês?
a) Nessa questão temos uma placa que está no plano , e que tem um formato vazado na extremidade.
Pra começar a resolução, esse item nos pede para determinar as coordenadas do centro de massa da placa.

Bora começar pelo mais simples! Como a placa está apenas no plano , temos .
Além disso, como podemos ver abaixo:
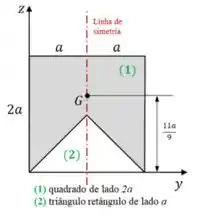
A placa é simétrica em relação ao eixo , de modo que .
Agora chegamos na parte um pouco mais complicada, o cálculo de .
A ideia nesses casos é sempre completar a placa com figuras geométricas conhecidas pra facilitar o cálculo.
Assim, podemos considerar que a área da placa é dada pela área do quadrado de lado subtraído do triângulo retângulo de lado . Daí, como a placa é homogênea:
Essa é a vantagem de usar figuras geométricas conhecidas (tipo quadrados, retângulos, triângulos, circunferências), pois conhecemos a posição dos centros geométricos. Temos:
(centro geométrico de um quadrado)
(centro geométrico de um triângulo)
Além disso, a área do quadrado e do triângulo valem, respectivamente:
Show! Substituindo tudo isso na nossa fórmula para cálculo de , temos:
Lembrando que:
Logo:
Logo:
Prontinho, achamos o centro geométrico da placa 😊
Passo 2
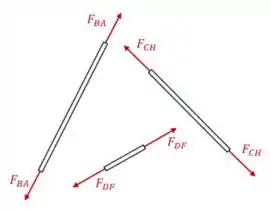
Agora devemos desenhar o diagrama de corpo livre (DCL) da placa e das barras.
Começando pelo das barras, deve agir uma força axial em cada uma delas. Vamos supor que essa força seja de tração. Assim, podemos desenhar:
Beleza! Agora vamos desenhar o DCL da placa. Precisamos considerar a força Peso atuando em , a força em e o momento do binário no eixo . Além disso, também temos as forças que as barras fazem na placa, e a reação do ponto , que ocorre nos eixos.
Assim, temos:
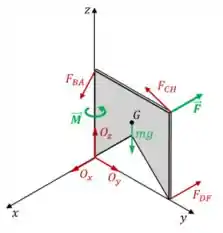
Prontinho 😊
Passo 3
c) Aqui devemos escrever as equações de equilíbrio da placa.
Como a placa está em equilíbrio estático, deve valer que:
Considerando os eixos e , temos:
Pensando nos momentos em relação a cada um dos eixos, também podemos escrever:
Massa! Essas são nossas equações de equilíbrio da placa.
Passo 4
d) Precisamos determinar os esforços atuantes nas barras.
É galera, não tem outro jeito de fazer isso, tem que resolver esse sistema...

De , temos:
De , temos:
Logo:
De , temos:
Perfeito, já descobrimos os esforços atuantes nas três barras. Como apenas deu um valor negativo, ela está comprimida enquanto as outras estão tracionadas.
Passo 5
e) Pra finalizar essa questão, precisamos apenas calcular as reações de apoio em . Relembrando nosso sisteminha de forças:
De , temos:
De , temos:
E, como os primeiros serão os últimos e os últimos serão os primeiros, de , vem:
Ufaa!! Terminamos de resolver o sistema e encontramos as três reações de apoio do ponto .
Então é isso galera, espero que vocês tenham gostado. Até a próxima 😉
Resposta
a)
b) Resolução no texto.
c) Resolução no texto.
d)
(compressão)
(Tração)
(Tração)
e)