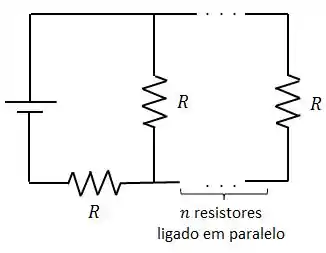
Na figura abaixo, um conjunto de resistores em paralelo é ligado em série a um resistor e a uma fonte ideal. Todos os resistores têm a mesma resistência.
Se um outro resistor de mesmo valor fosse ligado em paralelo com esse conjunto, a corrente na fonte variaria de .
Qual é o valor de ?
Passo 1
Beleza, vamos começar encontrando uma expressão para a corrente na fonte. Depois, nós vamos adicionar mais um resistor a esse arranjo, calcular a nova corrente e comparar as duas.
Beleza?
Então partiu!
Pra calcular a corrente na fonte, utilizamos a Lei de Ohm para a resistência equivalente do circuito.
Para calcular a resistência equivalente, vamos começar pelo arranjo que resistores em paralelo.
Como se tratam de resistores, nós teremos termos no lado direito da igualdade acima. Logo:
Por fim, a resistência equivalente do sistema será:
Passo 2
Com a resistência equivalente calculada, a corrente na fonte será dada por:
Passo 3
Show! Agora vamos adicionar mais um resistor ao arranjo de resistores em paralelo e calcular a nova corrente .
Seguindo o mesmo raciocínio que usamos anteriormente:
Agora, como temos resistores, teremos termos no lado direito da igualdade.
Assim, a resistência equivalente do circuito será:
Passo 4
Agora, a nova corrente na fonte será:
Passo 5
O problema falou que, quando adicionamos mais um resistor ao arranjo de resistores, a diferença de corrente é de . Logo:
Agora vamos substituir tudo, arrumar e ver se conseguimos resolver a nossa vida aqui.
Logo de cara, pra simplificar isso aqui, podemos sumir com todos os nos numeradores de com os dos denominadores.
Antes de você ficar tenso porque tem um monte de número com vírgula e calcular os valores de vai ser um saco, tem um jeito de tentar simplificar um pouco isso aqui.
Pra começar, vamos multiplicar todos os termos por pra sumir com as vírgulas:
Agora podemos dividir todos os termos por que é o máximo divisor comum a todos esses caras:
Agora só temos que encontrar a solução dessa equação de segundo grau usando Bhaskara.
Resolvendo isso, vamos achar 2 valores de .
Só que o valor de não pode ser negativo. Logo: