Exercícios de Dilatação Térmica - Lista de Exercícios Resolvida

Um cilindro, com coeficiente de dilatação , está muito apertado preso em um plano cujo coeficiente de dilatação é . Para afrouxarmos o cilindro devemos (considere ambos os coeficientes de dilatação positivos).

Aumentar a temperatura do sistema.

Diminuir a temperatura do sistema.

Aumentar apenas a temperatura do cilindro.

Como , a única forma de liberarmos o cilindro é quebrando o plano.

Nenhuma das afirmativas anteriores.

Uma barra de aço tem de diâmetro a . Um anel de latão tem um diâmetro interno de a . Se os dois objetos são mantidos em equilíbrio térmico, a que temperatura barra se ajusta perfeitamente o furo? Sabendo que o coeficiente linear de dilatação do aço é e o do latão é .

Logo após a Terra ter sido formada, o calor liberado pelo decaimento dos elementos radioativos elevou a temperatura média interna de para , cujo valor aproximado permanece até hoje. Admitindo um coeficiente de dilatação volumétrica médio de , de quanto o raio da Terra aumentou desde sua formação?

Um furo em uma placa de alumínio tem de diâmetro a . Qual é o diâmetro do furo quando a temperatura da placa é aumentada para ? Sabendo que o coeficiente linear do alumínio é

A , uma barra tem exatamente de comprimento, de acordo com uma régua de aço. Quando a barra e a régua são colocadas em um forno a , a barra passa a medir cm de acordo com a mesma régua. Qual é o coeficiente de expansão linear do material de que é feita a barra, sabendo que o do Aço é de ?

Verifica-se que uma barra de aço, de de comprimento à , dilata-se quando aquecida à .

Calcule para ele:

Seu coeficiente médio de dilatação linear

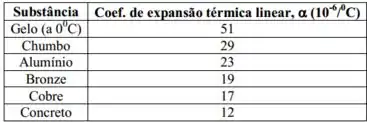
Quando a temperatura de um cilindro é aumentada de pra , seu comprimento aumenta

Com o auxilio da tabela abaixo, encontre de qual material o cilindro é feito.

Determine a variação percentual na densidade desse cilindro.

Como resultado de um aumento de , uma barra com uma rachadura no centro dobra para cima (figura abaixo). Se a distância fixa é e o coeficiente de dilatação linear da barra é , determine a altura do centro da barra.

Quando a temperatura de uma moeda de cobre é aumentada de o diâmetro aumenta de . Com precisão de dois algarismos significativos, determine o aumento percentual da área, da espessura, do volume e da massa especifica da moeda. Calcule o coeficiente de dilatação linear da moeda.

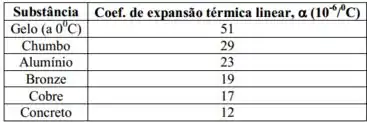
Quando a temperatura de um cilindro é aumentada de pra , seu comprimento aumenta

1. Com o auxilio da tabela abaixo, encontro de qual material o cilindro é feito.
2. Determine a variação percentual na densidade desse cilindro.

Um cilindro, com coeficiente de dilatação , está muito apertado preso em um plano cujo coeficiente de dilatação é . Para afrouxarmos o cilindro devemos (considere ambos os coeficientes de dilatação positivos).

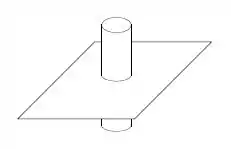
1. Aumentar a temperatura do sistema.
2. Diminuir a temperatura do sistema.
3. Aumentar apenas a temperatura do cilindro.
4. Como , a única forma de liberarmos o cilindro é quebrando o plano.
5. Nenhuma das afirmativas anteriores.

Um fio com de comprimento e de diâmetro sofre um alongamento de quando submetido a uma força de em uma das extremidades, com a outra extremidade fixa. Se um fio exatamente igual, exceto pelo fato de que possui um comprimento de , for submetido à mesma força, qual será a dilatação?

a) ;

b) ;

c);

d) ;

e) ;

Duas barras são feitas de latão e têm o mesmo comprimento. A seção reta de uma das barras é circular, com diâmetro . A outra tem seção reta quadrada, com lado . As barras pendem verticalmente de um suporte e têm um bloco de massa pendurado na extremidade inferior. Qual das duas barras sofre um alongamento maior, causado pela presença do bloco?

a) a barra de seção reta circular;

b) a barra de seção reta quadrada;

c) as duas barras sofrem o mesmo alongamento;

d) não é possível responder sem conhecer os valores numéricos de a e de m;

e) não é possível responder sem conhecer o comprimento das barras;

Considere um líquido homogêneo que tem massa específica à temperatura . Seja o coeficiente de dilatação volumétrica do líquido. Pode-se afirmar que a variação na massa específica do mesmo para uma variação da temperatura é:

Um recipiente de um material de coeficiente de dilatação linear está completamente cheio de um líquido cujo coeficiente de dilatação é . Como a temperatura deve variar para que o líquido transborde?

Escolha uma opção:

a. A temperatura deve diminuir pois o recipiente se dilata mais rápido que o líquido. 

b. A temperatura deve diminuir pois o coeficiente de dilatação linear do recipiente é menor que do líquido.

c. A temperatura deve aumentar pois o coeficiente de dilatação volumétrica do recipiente é maior que do líquido.

d. Como líquidos sempre se dilata mais que sólidos, a temperatura deve diminuir.

e. A temperatura deve aumentar pois o coeficiente de dilatação linear do recipiente é menor que o do líquido.

.

Um cilindro de germânio com massa se encontra na temperatura . O cilindro recebe então uma quantidade de calor . Determine o aumento de volume resultante.

Escolha uma opção:

Nenhuma das respostas apresentadas

Se, quando a temperatura de uma moeda de cobre aumenta de 100 , o diâmetro da moeda aumenta de 0,17%, a área de uma das faces da moeda aumenta de:

a) 0,34%;

b) 0,17%;

c) 0,51%;

d) 0,13%;

e) 0,27%;

A figura mostra três placas metálicas retangulares. Suas dimensões estão especificadas, sendo (Placa 1), (Placa 2) e (Placa 3), bem como seus respectivos coeficiente de expansão linear: ,e . Se todas sofrem a mesma variação de temperatura, assinale a opção correta:

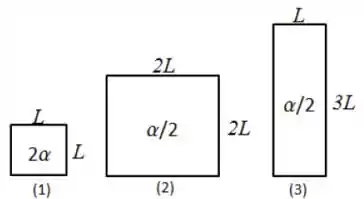
a) A dimensão vertical da placa 1 é a que mais aumenta e a área da placa 3 é a que mais aumenta;

b) A dimensão vertical da placa 2 é a que mais aumenta e a área da placa 1 aumenta tanto quanto a área da placa 2;

c) A dimensão vertical da placa 3 é a que mais aumenta e a área da placa 1 é a que mais aumenta;

d) A dimensão vertical da placa 1 é a que mais aumenta e a área da placa 2 aumenta tanto quanto a área da placa 1;

e) A dimensão vertical da placa 3 é a que mais aumenta e a área da placa 2 é a que mais aumenta.

Duas berras retilíneas idênticas, bastante finas, de comprimentos são unidas por suas extremidades, formando um angulo de entre si (veja figura ao lado). Ambas as barras tem coeficientes de dilatação linear dados por .

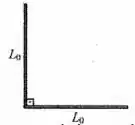
(a) (1,5) Se as barras são submetidas a uma variação de temperatura , calcule a soma dos comprimentos das barras após este processo. Expresse seu resultado em termos de , e .

(b) (2,0) Calcule a variação de temperatura a que deve ser submetida uma terceira barra, também de comprimento e de coeficiente de dilatação linear para que as duas barras resultantes do processo descrito no item (a) e esta terceira barra formem um triangulo retângulo. Expresse seu resultado em termos de e .

Considere duas chapas finas com áreas e , feitas de materiais isotrópicos com coeficientes de dilatação linear térmica respectivamente dados por e . Quando submetidas a um aumento de temperatura , qual o coeficiente de dilatação térmica superficial que atribuiremos à chapa composta cuja área inicial é ?

(a)

(b) ()/()

(c) ()/(2)

(d) 2()

(e)

(f) ()/2

(g) Não é possível determinar com os dados do enunciado.

Quando uma barra de comprimento é submetida a um certo aumento de temperatura, o comprimento da barra aumenta de um certo valor. Se uma barra de mesmo material de comprimento é submetida ao mesmo aumento de temperatura, qual é a relação entre a variação de comprimento da barra menor e a variação de comprimento da barra maior?

(a)

(b)

(c)

(d)

(e)

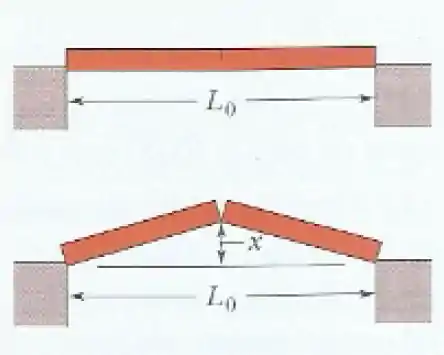
Uma barra homogênea com coeficiente de dilatação linear , mantida entre dois suportes rígidos com coeficiente de dilatação desprezível, é submetida a uma variação de temperatura T e, como resultado, se parte na sua metade, como mostrado na figura.

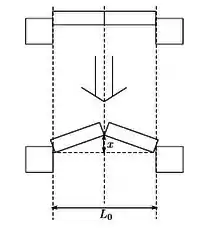
Considerando que a variação de temperatura é pequena quando comparada à temperatura inicial (), a altura x atingida pelo centro da barra pode ser escrita como:

a)

b)

c)

d)

e)

f)

O comprimento , a variação da temperatura e a variação do comprimento , respectivamente, estão dados para quatro barras:

Barra A:

Barra B:

Barra C:

Barra D:

Ordene as barras de acordo com os coeficientes de expansão térmica, começando pelo maior.

1. A e B empatados, depois C, D;
2. C, B, D, A;
3. B, A, D, C;
4. A, B, C, D;
5. C, depois A, B e D empatadas;

Inicialmente a uma certa temperatura um bloco de densidade e coeficiente de dilatação volumétrica está parcialmente submerso em um líquido de densidade volumétrica e coeficiente de dilatação volumétrica . Considere que nesta situação a razão entre o volume submerso e o volume total do bloco seja . Após uma variação de temperatura , ambos o bloco e o líquido irão se dilatar de forma que o bloco continua parcialmente submerso. A nova razão entre o volume submerso e o volume total do bloco será:

(a)

(b)

(c)

(d)

Uma barra homogênea é aquecida de até Sabendo-se que o comprimento inicial da barra é e que o coeficiente de dilatação linear da barra vale , podemos afirmar que a dilatação ocorrida, em, é igual a:

Um bloco cúbico de aresta a, feito de material homogêneo com densidade, está totalmente imerso em um fluido com densidade constante, em equilíbrio hidrostático e térmico à temperatura , como mostra a figura. Em seguida o conjunto é aquecido até atingir o equilíbrio na temperatura . Considerando que o coeficiente de dilatação volumétrica do fluido é e o coeficiente de dilatação volumétrica do bloco é , e que a aceleração da gravidade é uniforme com módulo , responda:

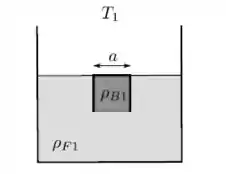
a) Obtenha a densidade do bloco em termos da densidade do fluido à temperatura .

b) Obtenha a densidade do fluido à temperatura .

c) Obtenha a densidade do bloco à temperatura .

d) Com base nos seus cálculos diga se, após a mudança de temperatura o bloco continuará flutuando totalmente submerso como na figura, apenas parcialmente submerso ou afundará totalmente, repousando sobre o fundo do recipiente. Justifique sua resposta.

Uma barra de aço (Coeficiente de dilatação linear ) tem de diâmetro a . O anel de cobre (Coeficiente de dilatação linear ) tem um diâmetro interno de (Veja a Fig. ) e possui a mesma temperatura da barra. Se os dois objetos são mantidos em equilíbrio térmico, a que temperatura a barra se ajusta perfeitamente ao furo do anel, de acordo com a Fig. abaixo?

.

.

. Nenhuma das alternativas

.

.

.

.

.

As tampas dos recipientes de vidros são mais facilmente removidas quando o conjunto é imerso em água quente, tal fato ocorre porque.

1. O metal dilatasse mais que o vidro quando ambos são sujeitos a mesma variação de temperatura
2. A água quente amolece o metal permitindo que a tampa se solte.
3. A água quente amolece o vidro, permitindo que a tampa se solte
4. N.R.A
5. A água quente lubrifica a superfície de contato, reduzindo o atrito entre elas.

Uma barra de aço (Coeficiente de dilatação linear ) tem de diâmetro a . O anel de cobre (Coeficiente de dilatação linear ) tem um diâmetro interno de (Veja a Fig. ) e possui a mesma temperatura da barra. Se os dois objetos são mantidos em equilíbrio térmico, a que temperatura a barra se ajusta perfeitamente ao furo do anel, de acordo com a Fig. abaixo?

.

.

.

. Nenhuma das alternativas

.

.

.

.

Para qualquer temperatura a diferença entre os comprimentos de duas barras com coeficientes de expansão linear e é a mesma. Para que isto seja válido, a relação entre os respectivos comprimentos deve ser igual a:

(a)

(b)

(c)

(d)

. Um bloco de latão na forma de um cubo possui massa . Determine a área da face do cubo após o material sofrer uma variação de temperatura de .

DADOS:

coeficiente de dilatação linear

densidade do concreto

.

.

.

.

. nenhuma das respostas apresentadas

.

.

.

. Um bloco de concreto na forma de um cubo possui massa . Determine a área da face do cubo após o material sofrer uma variação de temperatura de .

DADOS:

coeficiente de dilatação linear

densidade do concreto

.

.

.

. nenhuma das respostas apresentadas

.

.

.

.

Um dispositivo eletrônico esférico e de diâmetro igual a 2cm foi afixado na junção entre dois trilhos de alumínio de 2m de comprimento cada a temperatura de . A junção mantém os trilhos separados a 3cm. Determine qual a temperatura necessária para que a dilatação dos trilhos inicie o esmagamento do dispositivo eletrônico. .

Um bloco de cobre na forma de um cubo possui massa . Determine a área da face do cubo após o material sofrer uma variação de temperatura de .

DADOS:

coeficiente de dilatação linear

densidade do cobre

Escolha uma opção:

Nenhuma das respostas apresentadas

Por que um copo de vidro às vezes quebra quando se despeja rapidamente água fervendo no mesmo?

1. A água quente dilata, empurrando o copo para fora.
2. A água quente resfria quando toca o copo, encolhendo e puxando o copo para dentro.
3. O copo fica quente e dilata, causando a quebra de suas moléculas.
4. A região interna do copo dilata mais rapidamente do que a região externa, causando a quebra do mesmo.
5. Nenhuma das respostas anteriores.