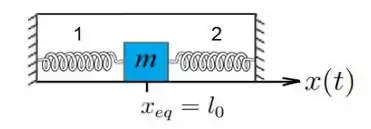
Um bloco de massa , preso a duas molas idênticas, com comprimentos naturais iguais a e constantes elásticas iguais a , estão dentro de um recipiente com um líquido, cujo coeficiente de atrito viscoso vale . Uma força harmônica de amplitude e frequência angular atua sobre o bloco ao longo da direção horizontal. O atrito entre o bloco e o fundo do recipiente é desprezível. Usando o referencial da figura, determine:
A solução da equação de movimento no regime estacionário, em função de , considerando :
(a)
(b)
(c)
(d)
(e)
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado nos deu um arranjo com duas molas que tem comprimentos naturais e constantes elásticas iguais, essas molas estão presas a um bloco e os três objetos estão dentro de um recipiente com um líquido de atrito viscoso. Então, nós temos uma força harmônica e uma frequência angular que age sobre o bloco e nós queremos determinar a solução da equação de movimento no regime estacionário.

Mas o quê que isso quer dizer? Lembra do movimento harmônico amortecido? Nele a gente tem uma força de amortecimento que “atrapalha” a oscilação do sistema. No nosso caso, essa força é a força viscosa do fluido. Mas além disso, nós também temos uma força externa que afeta a oscilação. Então, nós temos um sistema com oscilador forçado e amortecido.
Quê isso interfere nos cálculos da equação do movimento? Interfere em tudo rs. Porque nós temos que considerar todas as forças que estão atuando no sistema. Nesse caso, temos a força viscosa , a força externa oscilatória que é definida como e a força elástica igual a .
Usando a segunda Lei de Newton (), o somatório dessas forças nos fornece a equação:
Repare que essa é uma equação diferencial ordinária (EDO) não homogênea, e representa a equação do movimento harmônico forçado e amortecido. Pra encontrar uma solução para essa EDO precisamos descobrir uma solução para a parte homogênea, , e uma solução particular . Só que para tempos longos, a solução da equação homogênea vai tender a zero, então, a solução dessa equação diferencial vai ser expressa da seguinte maneira:
Onde indica a frequência da força externa, e tanto (que é a amplitude de oscilação) e (que é a fase) dependem de . Esses parâmetros são dados por:
E
A dedução dessas equações é bem complicadinha, porque envolve alguns conhecimentos de EDO’s não homogênea e o conhecimento dos parâmetros físico que a gente tá considerando. Mas o importante pra gente, nesse caso, é apenas descobrir o valor de e no sistema, pra obter uma solução da equação de movimento no regime estacionário.
Então, vamos lá!
Passo 2
O enunciado nos deu a frequência da força externa e a força externa , que atuam sobre o bloco de massa . é definido pela razão entre o coeficiente de atrito viscoso e a massa, então:
Além disso, no caso do sistema massa mola, a frequência dos sistema, , é igual a e . Logo:
Substituindo esses dados na equação da amplitude, temos:
Colocando o denominador em notação científica:
Tirando a raiz no denominador:
Logo, nossa amplitude será:
Passo 3
Agora calculando a fase de oscilação, por meio da expressão:
Nós temos , e . Substituindo na equação:
Logo, temos:
Passo 4
Conhecendoe e podemos determinar a solução da equação de movimento no regime estacionário em função de :
Substituindo os valores na equação:
Que é a alternativa (A).
Valeu, galera! Até a próxima! 😉