Dois blocos A e B,de massas e , respectivamente, estão colocados um sobre o outro conforme a figura abaixo. O bloco A está ligado a uma mola de constante elástica . A mola não está em posição de equilíbrio e sim está destendida de um valor do seu valor de equilíbrio conforme a figura. Os coeficientes de atrito estático entre as superfícies do bloco B e o chão e entre as superfícies do bloco A e B são e , respectivamente.
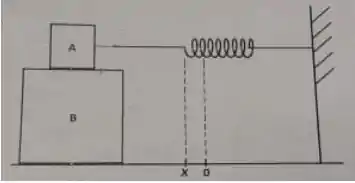
(a) Desenhe o diagrama de forças que agem separadamente nos blocos A e B.
(b) Suponha que , e que todo o sistema esteja em repouso.
. Escreva as equações de movimento para o bloco A e a força de atrito entre o bloco A e B.
. Escreva as equações de movimento para o bloco B e as forças de atrito entre o bloco B e o chão.
. Quais são os pares de ação e reação?
. Determine , em função de , , , , e de modo que a força de atrito entre o bloco B e o chão seja máxima.
(c) Suponha que , e que todo o sistema esteja em repouso. Determine em função de , , , , e , de modo que a força de atrito entre o bloco B e o bloco A seja máxima.
Passo 1
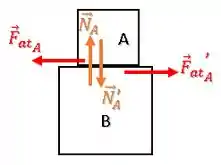
Vamos começar com o diagrama de forças sobre cada um dos blocos.
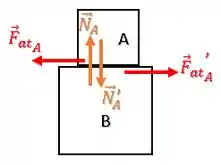
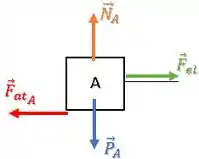
Bloco A:
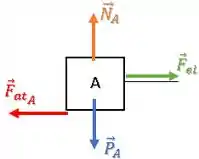
Primeiramente temos uma força peso para baixo e uma força normal apontando para cima.
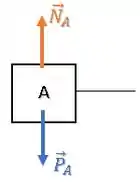
Além disso, a mola presa ao bloco A está distendida (esticada), ou seja, ela está puxando o bloco A com uma força elástica :
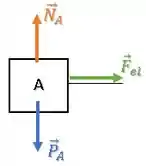
Essa força elástica tende a fazer o bloco A deslizar para a direita.
Portanto, a força de atrito vai atuar contra essa tendência, ou seja, para a esquerda:
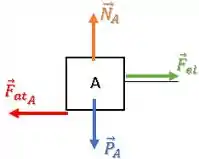
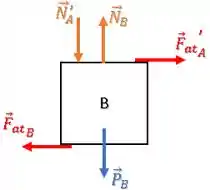
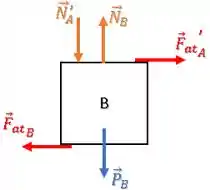
Bloco B:
Temos uma força peso e uma força normal (o chão exerce sobre o bloco B):
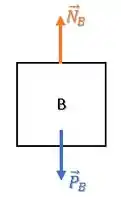
Além disso, se o bloco B exerce uma força de atrito e uma força normal sobre o bloco A, temos as reações dessas forças agindo sobre ele mesmo.
Ou seja, a força de atrito que o bloco A exerce sobre B e a força normal que o bloco A exerce sobre o bloco B (mesmo módulo e sentidos opostos):
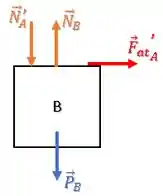
OBS: Podemos representar tanto em cima quanto em baixo do diagram do bloco B, o importante é que ela aponte na direção correta (para baixo).
Por último, temos uma força de atrito que o chão exerce sobre o bloco B.
Ele vai contra a tendência de deslizamento do bloco B, portanto ele atua para a esquerda:
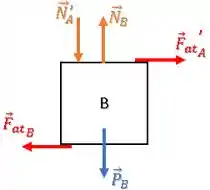
O item (a) está respondido.
Passo 2
(b) Suponha que , e que todo o sistema esteja em repouso.
. Escreva as equações de movimento para o bloco A e a força de atrito entre o bloco A e B.
Para isso, basta aplicar a Segunda Lei de Newton para o bloco A:
Como ele está em repouso, temos que:
Assim, podemos dizer que nos dois eixos a força resultante é nula:
No eixo , temos:
Como a força elástica é dada pela constante elástica vezes a deformação da mola, temos que:
No eixo , temos:
Passo 3
. Escreva as equações de movimento para o bloco B e as forças de atrito entre o bloco B e o chão.
Vamos fazer o mesmo que no item anterior. Vamos aplicar a Segunda Lei de Newton para o bloco B:
Como ele está em repouso, temos que:
No eixo , temos:
A força de reação apresenta o mesmo módulo de , portanto:
No eixo , temos:
Novamente, é a reação de , então elas apresentam o mesmo módulo que já calculamos :
Passo 4
. Quais são os pares de ação e reação?
Pelo princípio de ação e reação (terceira Lei de Newton), quando vc exerce uma força sobre um corpo, esse corpo exerce uma força de mesma intensidade sobre você.
Portanto, o contato entre os blocos forma dois pares de ação e reação. O primeiro deles é a partir da força normal e ) e o segundo da força de atrito ( e ).
Passo 5
. Determine , em função de , , , , e de modo que a força de atrito entre o bloco B e o chão seja máxima.
Uma força de atrito estático apresenta seu valor máximo quando:
Portanto, se queremos que seja máxima, temos que ela valerá o coeficiente de atrito estático entre a superfície do bloco B e o chão vezes a força normal nessa superfície :
Já sabemos o valor de em função das variáveis do problema:
Passo 6
Queremos achar para essa situação, então vamos utilizar a expressão da Segunda Lei de Newton na horizontal para o bloco B:
Substituindo a expressão da força de atrito:
Isso significa que para esse valor de deformação , a força de atrito impedindo o bloco B de deslizar estará em seu valor limite.
Passo 7
(c) Suponha que , e que todo o sistema esteja em repouso. Determine em função de , , , , e , de modo que a força de atrito entre o bloco B e o bloco A seja máxima.
Se queremos que seja máxima, ela valerá o coeficiente de atrito estático entre a superfície dos blocos vezes a força normal nessa superfície :
Já sabemos o valor de em função das variáveis do problema:
Passo 8
Queremos achar para essa situação, então vamos utilizar a expressão da Segunda Lei de Newton na horizontal para o bloco A:
Substituindo a expressão da força de atrito:
Isso significa que para esse valor de deformação , a força de atrito impedindo o bloco A de deslizar estará em seu valor limite.
Resposta
(a)
(b)
.
.
.
e
e
.
(c)