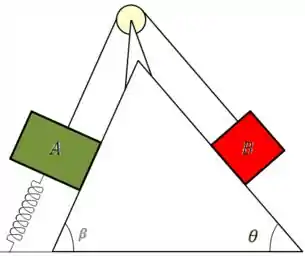
Temos dois blocos e dispostos em uma cunha presos entre si por um fio, enquanto o bloco está preso ao chão por uma mola de constante elástica , como mostrado na figura abaixo. Sabendo que suas massas são e , respectivamente e que o atrito é desprezível. Determine a deformação da mola e a força de tração no fio, sabendo que os blocos estão em repouso. Considere ainda os ângulos mostrados na figura como dados, e o módulo da aceleração da gravidade como .
Passo 1
Normalmente começamos um problema com vários blocos, fazemos o DCL do sistema. Neste caso, como temos os blocos em repouso, ou seja, em equilíbrio fazer o sistema pode ser algo mais complicado, então iremos montar as equações para cada bloco.
Os dados do problema são
Em problemas literais é sempre bom escrever os dados separados para mais tarde conferir se as respostas estão de acordo com esses dados.
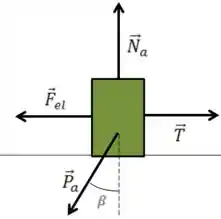
Para o bloco
Vamos responder as perguntas do passo a passo para colocar as forças
- A massa dele é considerada?
- Ela esta encostada em alguma superfície?
- Tem algum fio?
- Tem mola?
Sim, ele tem massa.
Sim, o bloco está apoiado na superfície inclinada.
Sim, existe um fio.
Não, não existe mola atuando.
Quando temos um exercício de plano inclinado, é mais fácil considerarmos a horizontal e vertical em relação à superfície inclinada, isso facilita nossas contas porque ele não tem movimento vertical em relação a essa superfície. O DCL ficaria
O ângulo fica na força peso com a vertical
Passo 2
Como o bloco está em equilíbrio, não faz diferença qual eixo vamos escolher para começar o problema, porem como a força que nos interessa é a tração, não precisamos fazer as contas ao longo do . No , que está em equilíbrio,
Devemos encontrar usando a “regra do COlado, SEparado”.
Passo 3
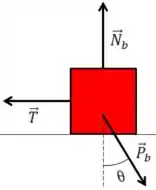
Para o bloco
Vamos responder as perguntas do passo a passo para colocar as forças
- A massa dele é considerada?
- Ela esta encostada em alguma superfície?
- Tem algum fio?
- Tem mola?
Sim, ele tem massa.
Sim, o bloco está apoiado na superfície inclinada.
Sim, existe um fio.
Sim, existe uma mola.
Quando temos um exercício de plano inclinado, é mais fácil considerarmos a horizontal e vertical em relação à superfície inclinada, isso facilita nossas contas porque ele não tem movimento vertical em relação a essa superfície. O DCL ficaria
O ângulo fica na força peso com a vertical
Nesse DCL temos um pequeno problema, como não sabemos qual bloco estaria descendo caso o bloco não estivesse preso no chão pela mola, vamos considerar o sentido da força elástica para esquerda, isso quer dizer q o bloco estaria descendo. Vamos ver como resolver esse problema de sentido já já.
Passo 4
No , como está em equilíbrio,
Devemos encontrar usando a “regra do COlado, SEparado”.
Como queremos que seja positivo basta colocarmos em módulo
Dessa forma garantimos que é positivo.