Exercícios de Força Elástica - Lista de Exercícios Resolvida
Questão 1
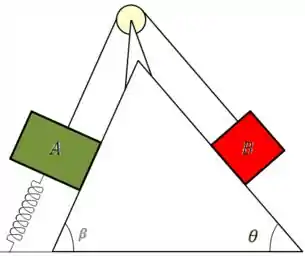
Temos dois blocos e dispostos em uma cunha presos entre si por um fio, enquanto o bloco está preso ao chão por uma mola de constante elástica , como mostrado na figura abaixo. Sabendo que suas massas são e , respectivamente e que o atrito é desprezível. Determine a deformação da mola e a força de tração no fio, sabendo que os blocos estão em repouso. Considere ainda os ângulos mostrados na figura como dados, e o módulo da aceleração da gravidade como .
Questão 2
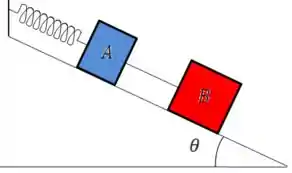
Dois blocos e , de massa e respectivamente, estão apoiados em um plano inclinado sem atrito. Eles estão presos entre si por um fio, enquanto o bloco é mantido em repouso por estar preso a parede por uma mola, tendo sua constante elástica igual a . Determine O valor da força de tração no fio e o valor da deformação da mola.
Questão 3
Para a verificação experimental das leis da Dinâmica, foi montado o sistema a seguir:
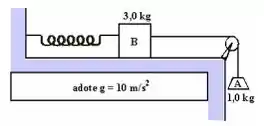
Nele, o atrito é desprezado, o fio e a aceleração são ideais. Os corpos A e B encontram-se em equilíbrio quando a mola “ultraleve” M está distendida de . A constante elástica dessa mola é:
Questão 4
O esquema apresenta um elevador que se movimenta sem atrito. Preso a seu teto, encontra-se um dinamômetro que sustenta em seu extremo inferior um bloco de ferro. O bloco pesa mas o dinamômetro marca . Considerando , podemos afirmar que o elevador pode estar:
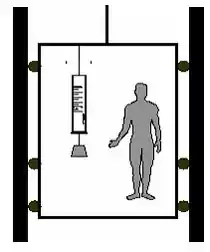
- Em repouso
- Descendo com velocidade constante
- Descendo em queda livre
- Descendo com movimento acelerado de aceleração de
- Subindo com movimento acelerado de aceleração de
Questão 5
1c) Na figura abaixo, está representado o gráfico de uma força variável unidimensional que atua sobre uma partícula de massa . Entre as posições e , a força pode ser escrita como , e entre 0 e a força é constante . Seja , , e . A partícula se movimenta no sentido positivo do eixo e no instante que passa pelo ponto sua velocidade é . Calcule a velocidade da partícula quando ela chega na posição . (Você deve incialmente encontrar para fazer a questão!).
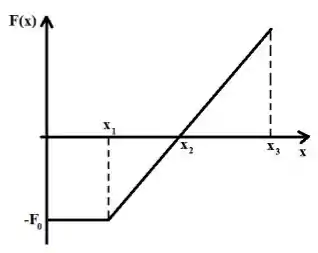
Questão 6
3) Um elevador tem a mesma aceleração, na subida e na descida. Uma mola presa ao teto do elevador carrega uma massa de . A constante elástica da mola é . Quando o elevador acelera na subida, a mola apresenta um comprimento de . Quando acelera na descida a mola apresenta comprimento de . (b) quanto a mola distende quando a aceleração é nula?
Ver solução completaQuestão 7
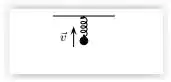
Uma bolinha pendurada na extremidade de uma mola vertical executa um movimento oscilatório. Na situação da figura, a mola encontra-se comprimida e a bolinha está subindo. Sendo a força da mola e a força peso aplicadas na bolinha, o único esquema que pode representar tais forças na situação descrita é:

Questão 8
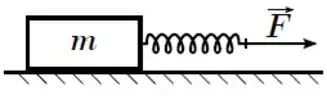
Um bloco de massa é puxado por uma mola ideal em movimento retilíneo sobre uma superfície horizontal com aceleração constante de módulo . O coeficiente de atrito cinético entre o bloco e a superfície é . A elongação da mola é
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 9
8. Uma corda de comprimento e densidade , com ambas as extremindades ficas, oscila no quarto harmônico de uma onda estacionária de acordo com a seguinte equação:
Onde numa das extremindades da corda ( é dado em metros e em segundos).
Qual deve ser a tensão aplicada na corda para que ela oscle no segundo harmônico?
OBS: Adote que o valor de não se altera.
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 10
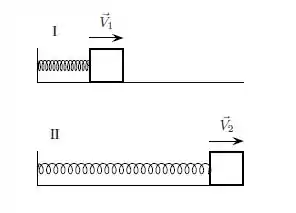
Um bloco, apoiado sobre uma superfície horizontal com atrito não desprezível, está preso a uma das extremidades de uma mola (que tem sua outra extremidade presa à parede), e executa um movimento oscilatório. Na posição representada na Figura I, a mola está comprimida de uma distância em relação ao seu comprimento natural. Em um instante posterior, ela encontra-se na posição representada na Figura II, com a mola distendida da mesma distância . Em ambas as situações o bloco está se movendo para a direita, com velocidades respectivamente iguais a e . Sendo e as forças exercidas pela mola sobre o bloco nas situações I e II, respectivamente, é correto afirmar que:
a) aponta para a direita, aponta para a esquerda e
b) aponta para a direita, aponta para a esquerda e
c) e apontam para a direita e
d) e apontam para a esquerda e
e) aponta para a esquerda, aponta para a direita e
f) aponta para a esquerda, aponta para a direita e
Ver solução completaQuestão 11
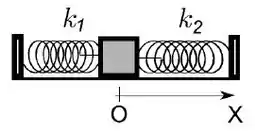
Um bloco de massa que pode se movimentar sem atrito sobre uma superfície horizontal está preso por duas molas de constantes elásticas e , como é mostrado na figura para a situação em que ele se encontra em equilíbrio. Ao ser deslocado de uma distância e posteriormente liberado passam a atuar no bloco as forças e devido às molas. Indique qual das afirmações está correta em relação à força resultante que atuará no bloco.: ( é o vetor unitário na direção horizontal OX):
(a) A força resultante será
(b) A força resultante será
(c) A força resultante será
(d)
(e)
(f) A força resultante será
(g) A força resultante será
Ver solução completaQuestão 12
3) Um elevador tem a mesma aceleração, na subida e na descida. Uma mola presa ao teto do elevador carrega uma massa de . A constante elástica da mola é . Quando o elevador acelera na subida, a mola apresenta um comprimento de . Quando acelera na descida a mola apresenta comprimento de . (a) Supondo a aceleração constante, calcule o módulo desta aceleração;
Ver solução completaQuestão 13
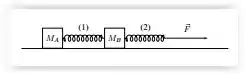
Dois blocos A e B, de massas MA = 3 kg e MB = 7 kg, estão apoiados sobre um plano horizontal sem atrito. Entre os corpos A e B, há uma mola ideal (1) de massa desprezível, e uma outra mola (2), idêntica a esta, se encontra presa ao outro lado do bloco de massa MB, como mostra a figura. Uma força constante horizontal é aplicada sobre a mola (2) puxando o conjunto para a direita de modo que os dois blocos se movem com a mesma aceleração. Sendo e as deformações das molas (1) e (2), respectivamente, é correto afirmar que:
Questão 14
Forças de tração de são aplicadas às duas extremidades de uma barra de de comprimento com de raio e um módulo de Young de . Em consequência, a barra sofre um alongamento de aproximadamente:
a) 0,64 mm;
b) 0,14 mm;
c) 0,020 mm;
d) 0,040 mm;
e) 1,42 mm
Ver solução completaQuestão 15
Em um bungee jumping, um elástico bastante comprido é amarrado aos pés de uma pessoa, que salta de uma plataforma e cai livremente até ser sustentado pelo elástico. Considere um elástico de tamanho e constante de elasticidade . Despreze a resistência do ar.
a) Desenhe um diagrama de forças que agem sobre a pessoa durante a queda;
b) Faça um gráfico da força resultante atuando na pessoa em função da distância à plataforma de salto;
c) Calcule a distância até a plataforma de salto em que a velocidade de queda é máxima;
d) Encontre a distância até a plataforma de salto em que a velocidade se anula.
Ver solução completaQuestão 16
[ENUNCIADO COMUM ÀS QUESTÕES 3 E 4]
Um bloco de massa é colocado sobre uma mola, de massa desprezível e constante elástica , que possui a outra extremidade fixa em uma superfície horizontal. Na figura (A), a mola está comprimida de em relação a sua posição não deformada. A figura (B) mostra o sistema depois de ter sido liberado, com o bloco atingindo uma altura máxima em relação à sua posição inicial [na figura (A)]. Considere
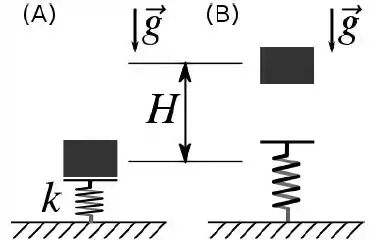
[QUESTÕES 3]
Suponha que o bloco desce suavemente sobre a mola, até atingir e permanecer em repouso na situação representada na figura (A). Qual o módulo, em , de ?
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Ver solução completaQuestão 18
Um bloco de massa encontra-se no chão, preso a uma mola, que tem sua outra extremidade presa a uma parede vertical. O bloco é liberado quando a mola encontra-se distendida e segue um movimento horizontal. Sabendo que não há atrito entre o bloco e o chão, sobre o movimento do bloco é correto afirmar que:
(a) A velocidade do bloco é nula quando a aceleração é máxima.
(b) A velocidade do bloco nunca é nula.
(c) A aceleração do bloco nunca é nula.
(d) A velocidade e aceleração do bloco se anulam nos mesmos instantes.
(e) A velocidade do bloco é máxima nos pontos de inversão do movimento do bloco.
(f) A velocidade do bloco é nula no ponto em que a mola está no seu comprimento natural.
Ver solução completaQuestão 19
. Uma mola uniforme, cujo comprimento sem distensão é , tem constante elástica . A mola é cortada em duas partes iguais de comprimento sem distensão cada uma. Qual o valor da constante elástica de cada um destes dois pedaços de mola?
Escolha uma:
Ver solução completaQuestão 20
Um corpo de , em equilíbrio, está preso a uma das extremidades de uma mola presa verticalmente, cuja constante elástica é . Considerando ², qual será a deformação da mola?
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 21
Um bloco de massa está parado sobre uma superfície, preso a uma mola presa a uma parede, como mostrado na figura abaixo; A mola tem massa desprezível, constante de mola e comprimento quando não está comprimida. O coeficiente de atrito estático entre o bloco e o chão é , e quando o bloco é colocado na posição , ele permanece em repouso na superfície. Espresse suas respostas em termos de , , , e constantes fundamentais.
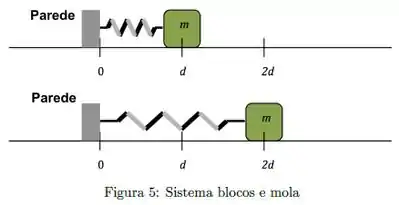
(a) Desenhe o diagrama de forças que agem no bloco quando ele está localizado na posição .
(b) Determine a força de atrito agindo sobre o bloco quando ele esta localizado na posição .
Ver solução completaQuestão 22
Dois blocos A e B,de massas e , respectivamente, estão colocados um sobre o outro conforme a figura abaixo. O bloco A está ligado a uma mola de constante elástica . A mola não está em posição de equilíbrio e sim está destendida de um valor do seu valor de equilíbrio conforme a figura. Os coeficientes de atrito estático entre as superfícies do bloco B e o chão e entre as superfícies do bloco A e B são e , respectivamente.
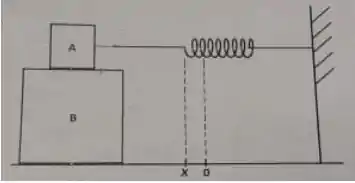
(a) Desenhe o diagrama de forças que agem separadamente nos blocos A e B.
(b) Suponha que , e que todo o sistema esteja em repouso.
. Escreva as equações de movimento para o bloco A e a força de atrito entre o bloco A e B.
. Escreva as equações de movimento para o bloco B e as forças de atrito entre o bloco B e o chão.
. Quais são os pares de ação e reação?
. Determine , em função de , , , , e de modo que a força de atrito entre o bloco B e o chão seja máxima.
(c) Suponha que , e que todo o sistema esteja em repouso. Determine em função de , , , , e , de modo que a força de atrito entre o bloco B e o bloco A seja máxima.
Ver solução completaQuestão 23
A figura abaixo mostra um sistema formado por um bloco (ou uma partícula) de massa e uma mola de constante elástica e comprimento de equilíbrio , ambos sob um plano inclinado que forma um ângulo com a horizontal. O bloco que não está conectado à mola, está inicialmente no ponto A e comprime a mola de uma distância . No instante inicial , o bloco é liberado e se movimenta ao longo do plano inclinado AE. Há atrito apenas no trecho plano BE (coeficiente de atrito cinético e estático ), a aceleração da gravidade é e o bloco permanece em contato com a superfície durante o movimento AE.
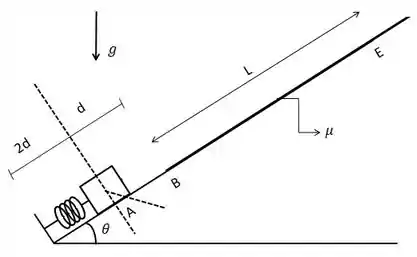
(a) Indique esquematicamente na figura abaixo as forças que atuam no bloco no instante inicial.
Questão 24
Temos uma definição, em particular, para a força da mola. Ela é dada por , onde é a constante de deformação da mola (específica para cada mola) e é a deformação da mola em .
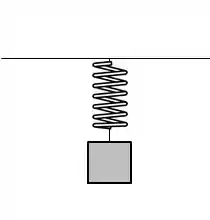
Mostramos um exemplo de um dinamômetro simples. Existem apenas duas forças atuando sobre o sistema que permanece em equilíbrio, são elas: a força peso e a força da mola.
Imaginemos que a massa desse corpo é de e deforma a mola em . A constante de deformação da mola, é:
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 25
Um bloco de massa , preso a duas molas idênticas, com comprimentos naturais iguais a e constantes elásticas iguais a , estão dentro de um recipiente com um líquido, cujo coeficiente de atrito viscoso vale . Uma força harmônica de amplitude e frequência angular atua sobre o bloco ao longo da direção horizontal. O atrito entre o bloco e o fundo do recipiente é desprezível. Usando o referencial da figura, determine:
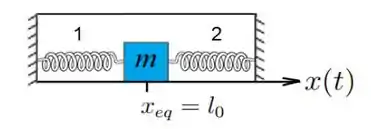
A frequência natural de oscilação, , do sistema vale:
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 26
Um bloco de massa , preso a duas molas idênticas, com comprimentos naturais iguais a e constantes elásticas iguais a , estão dentro de um recipiente com um líquido, cujo coeficiente de atrito viscoso vale . Uma força harmônica de amplitude e frequência angular atua sobre o bloco ao longo da direção horizontal. O atrito entre o bloco e o fundo do recipiente é desprezível. Usando o referencial da figura, determine:
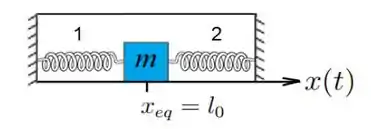
A expressão da força elástica que as molas exercem sobre o corpo, pode ser escrita como:
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 27
Um bloco de massa , preso a duas molas idênticas, com comprimentos naturais iguais a e constantes elásticas iguais a , estão dentro de um recipiente com um líquido, cujo coeficiente de atrito viscoso vale . Uma força harmônica de amplitude e frequência angular atua sobre o bloco ao longo da direção horizontal. O atrito entre o bloco e o fundo do recipiente é desprezível. Usando o referencial da figura, determine:
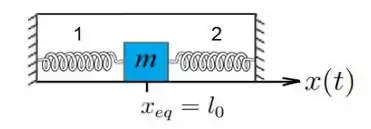
A solução da equação de movimento no regime estacionário, em função de , considerando :
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 28
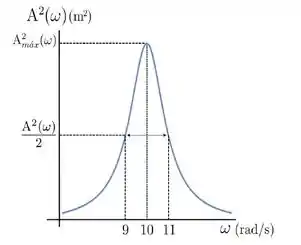
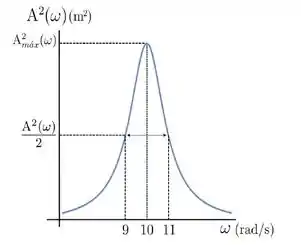
Considere um sistema mecânico de massa no regime de amortecimento fraco na presença de uma força externa , cuja curva de ressonância, com , é apresentada na figura:
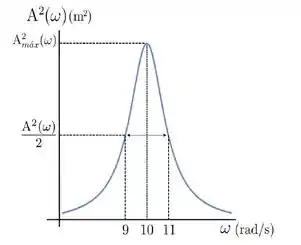
A constante de viscosidade vale:
(a)
(b)
(c)
(d)
(e)
Ver solução completa