Um corpo de massa move-se ao longo de um eixo , em um movimento unidimensional, sob a ação exclusiva de uma força conservativa . Essa força conservativa está associada à função energia potencial dada por (as unidades são o joule e o metro):
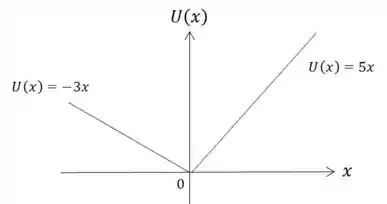
a) Esboce o gráfico da função energia potencial.
b) Uma energia mecânica de é fornecida ao corpo. Encontre os pontos de retorno à esquerda, , e à direita, . Encontre também a velocidade escalar do corpo quando ele está na posição
c) A velocidade escalar do corpo vale no ponto . Qual a energia mecânica associada ao sistema? E em que ponto a velocidade do corpo assumirá o valor ?
Passo 1
a)
Como a energia potencial é dada como uma equação do 1° grau em , então essa equação nada mais é que uma reta. Logo, basta lembrar-se das propriedades de uma reta (O sinal do coeficiente que acompanha o para determinar se a reta é crescente ou decrescente, e sua magnitude, pois quanto maior, mais inclinada é a reta.) e montar o gráfico.
Passo 2
b)
Lembrando que:
O ponto de retorno são os pontos em que . Para teremos:
Para temos:
Na posição , vamos ter:
Passo 3
c)
Aplicando novamente que:
Agora para descobrir onde a velocidade é , basta aplicar a fórmula novamente:
Resposta
a)
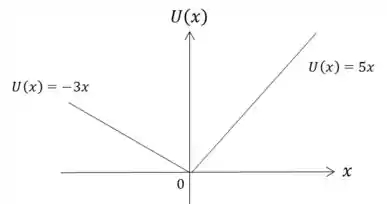
b) ; ;
c) ;